VECTORS

The Cartesian representation of a nD vector is a string of $n$ numbers that each represent a distance in a different direction/dimension. These directions are often referred to as "axes". $$ x = \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} $$ Vectors can be "scaled" by multiplying each element by a value $\alpha$ and two vectors $x$ and $z$ can be added element-wise (assuming they have the same length). $$ x\alpha = \begin{bmatrix} \alpha x_1 \\ \vdots \\ \alpha x_n \end{bmatrix}, \qquad x + z = \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} + \begin{bmatrix} z_1 \\ \vdots \\ z_n \end{bmatrix} = \begin{bmatrix} x_1+z_1 \\ \vdots \\ x_n+z_n \end{bmatrix} $$

AXES

The different directions or axes that make up a vector (scaled to have unit length) can be represented by the so-called "standard basis" vectors (more explanation of this name later). $$ I_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, \quad I_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix}, \quad \cdots \quad I_n = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}, $$

Drawing Vectors

Traditionally, axes are thought of as perpendicular to each other. The overall vector position of the vector $x$ is then the sum of each axis scaled by the appropriate element of $x$. $$ x = I_1 x_1 + \cdots + I_n x_n $$ $$ x = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} x_1 + \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} x_2 + \cdots + \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} x_n = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} $$ We can also visualize vectors using axes that are parallel to each other. In these settings, a vector can be thought of as a set of heights (possibly negative). These two depictions are shown below.

The Problem of Depth

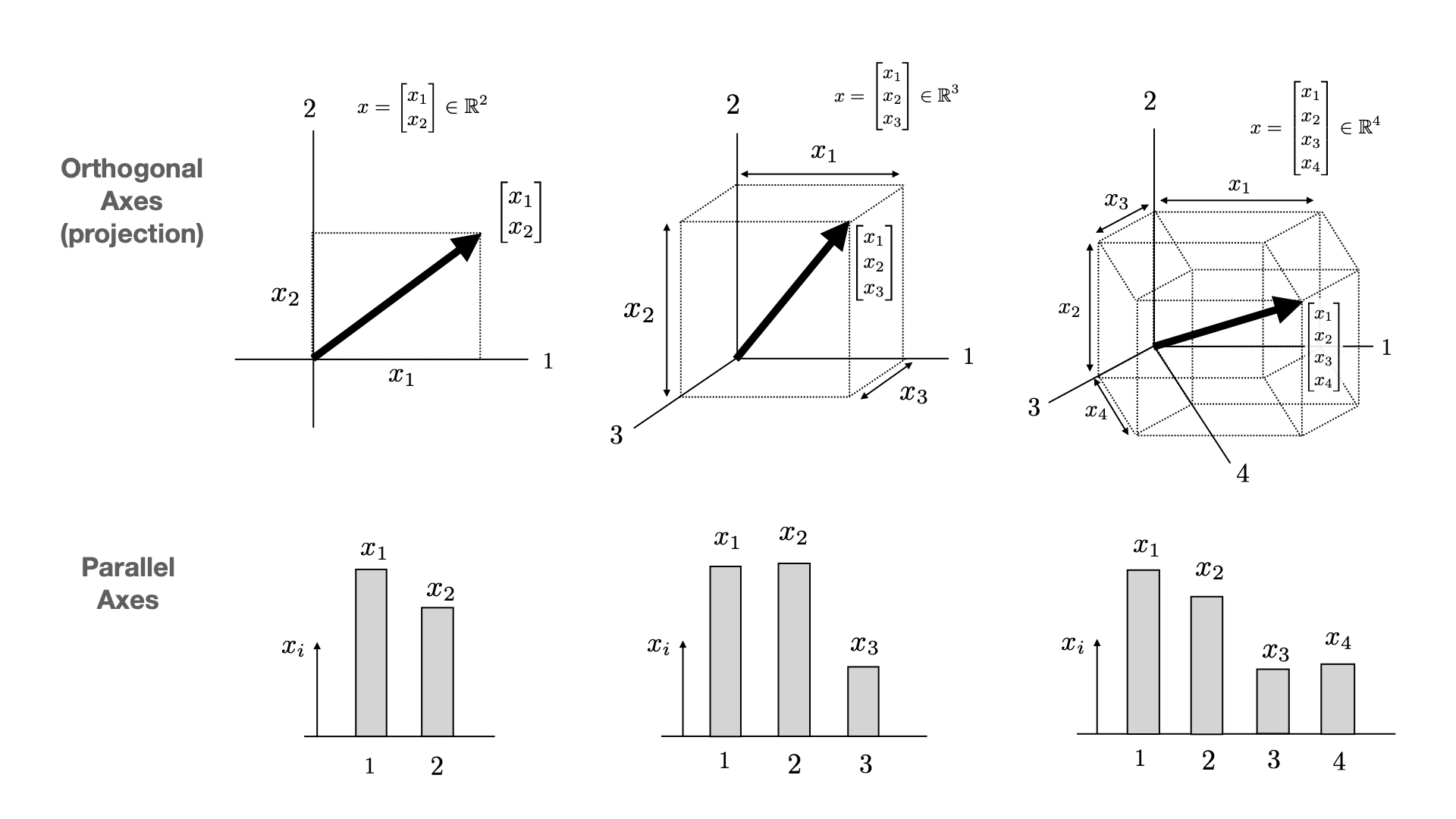
When trying to visualize perpendicular axes, we run into a problem. Since we can only draw in two dimensions, there are not enough perpendicular directions for all the axes for vectors of dimension three or higher. The best we can do is to pick directions (in the 2D image) for each of these axes to point and think of them as being perpendicular in some higher dimensional space. Our drawing then becomes a 2D projection of that higher dimensional space. This depiction does not lose any information for 2D vectors, but for 3D vectors, there is a depth direction (towards the viewer) that is lost in the drawing. Since we live in 3D, we are used to this and can often spatially reconstruct that lost direction in our mental representation of the vector. For 4D vectors, the depth "direction" becomes a plane; for 5D vectors, depth becomes a 3D space; for 6D vectors, depth becomes a 4D space, etc, and our drawing loses quite a bit of information and our intuition suffers accordingly. If you enjoy spatial reasoning, these 2D representations of higher dimensional vectors can still be useful, but you should be careful not to forget the information lost in the projection.

Paralle axis representations do not suffer from this pathology of depth, but this is simply because they do not attempt to leverage our spatial reasoning machinery for intuition at all.

More Intuition: Depth

For more intuition about the idea of depth in 2D representations of higher dimensional spaces, play around with the following visualizations of higher dimensional shapes. In particular, the jump from 3D to 4D (and then maybe 5D) can be illuminating.

More Drawing: Projection to 2D (Difficulty: 3/10)

The projection from an $n$D space to a 2D image can be represented by the matrix multiplication $y=Ax$ where $A \in \mathbb{R}^{2 \times n} $ $$ \underbrace{ \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}}_{2D} = \underbrace{ \begin{bmatrix} A_{11} & A_{12} & \cdots & A_{1n} \\ A_{21} & A_{22} & \cdots & A_{2n} \end{bmatrix} }_{2D \ axes \ representions} \underbrace{ \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}}_{nD} $$ Here $x \in \mathbb{R}^n$ is the coordinates of the vector in $n$D. Each column of the $n$ columns of $A$ is the representation of one of the $n$ axes in the 2D drawing and $y \in \mathbb{R}^2 $ is the 2D projection of the vector $x$. The depth directions (in the $n$D space) are given by the nullspace of the matrix $A$. The rank-nullity theorem then gives that depth has the dimension $n-2$. For a given vector $x$, the 2D projection $y$ is fully determined; however any $y$ can represent multiple points in the $x$ space (given by adding an arbitrary element in the depth directions). If one wanted to select an $x$ given a $y$, a simple way would be to choose $x$ with no depth component which would be the minimum norm solution $$ x = A^T(AA^T)^{-1}y $$