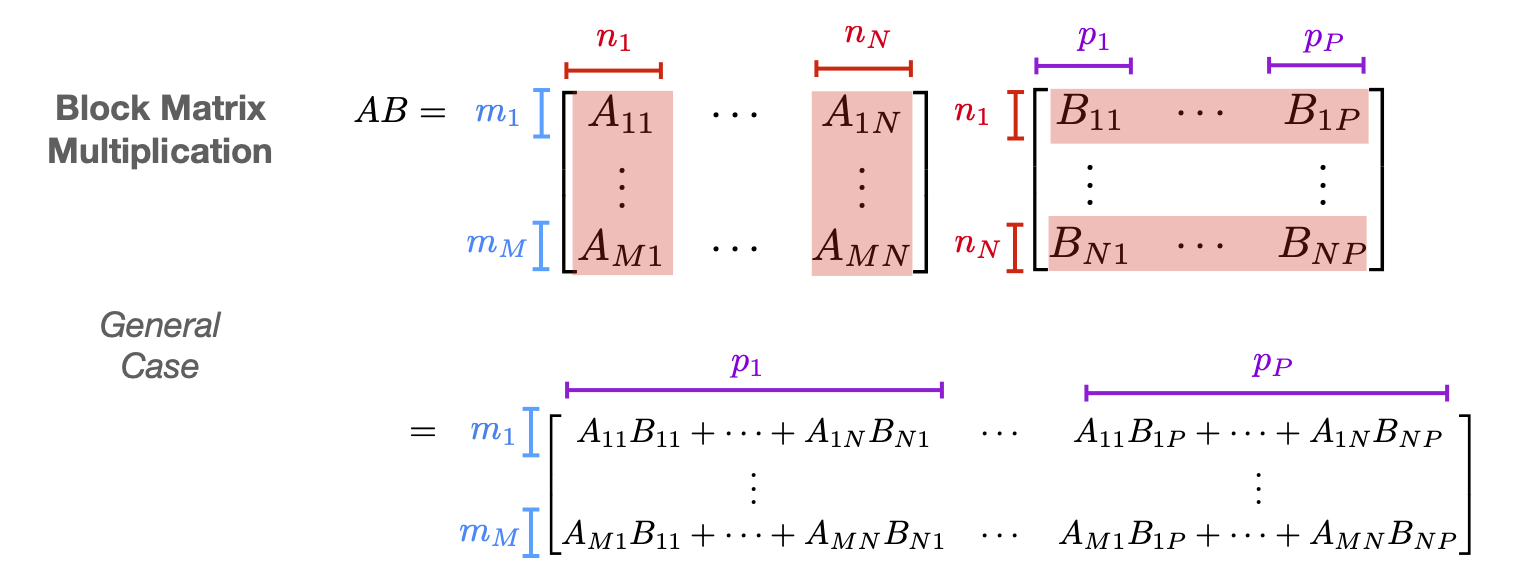
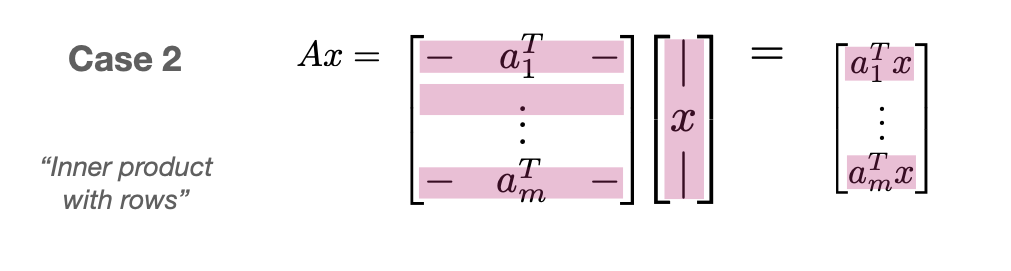
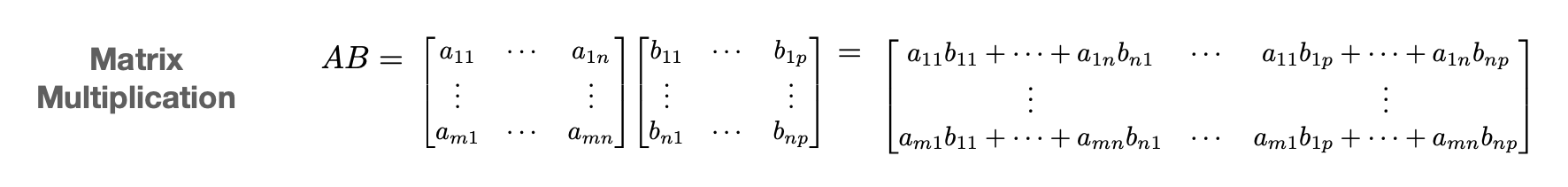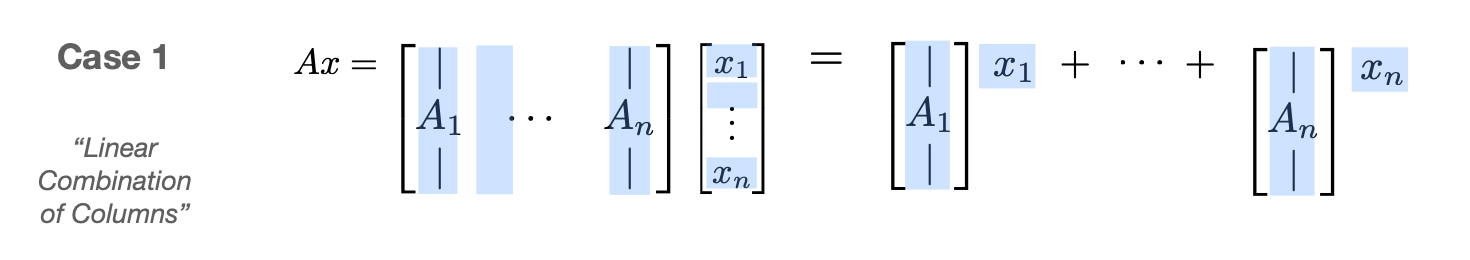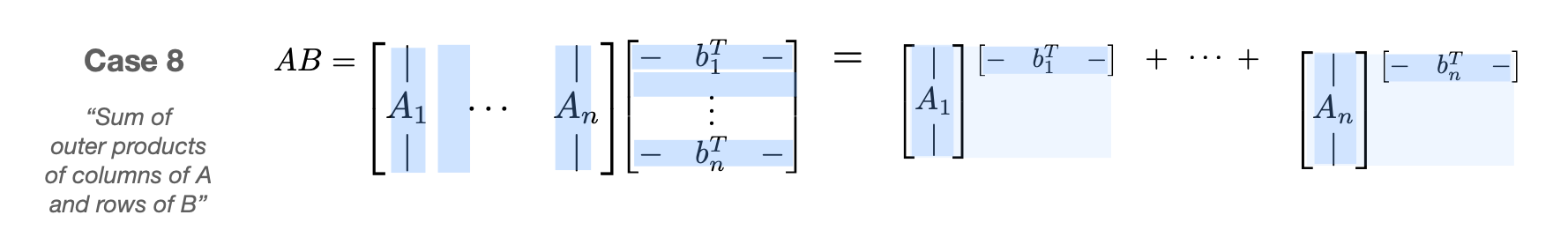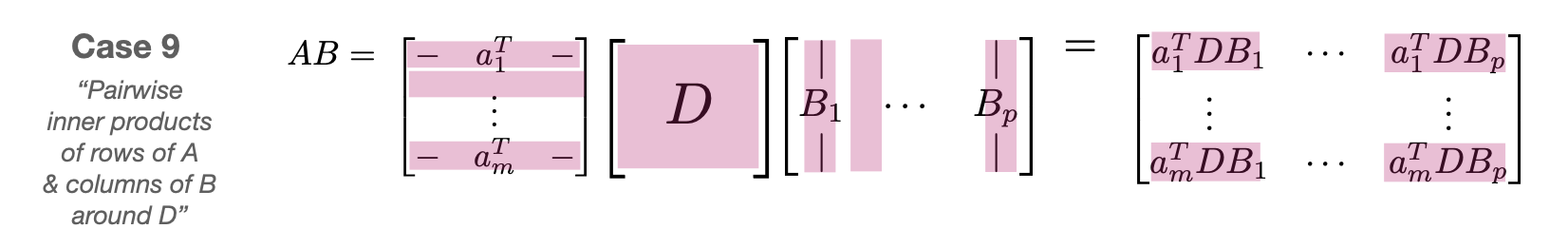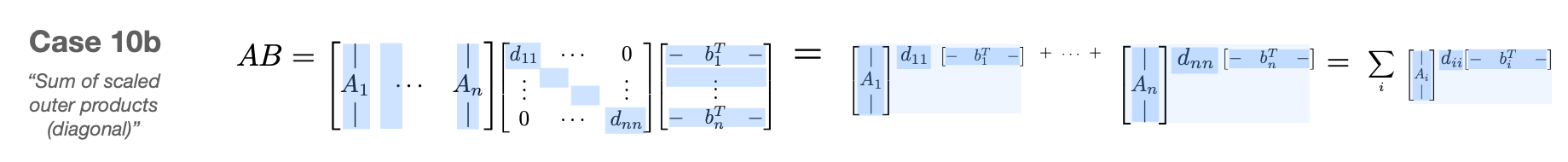$$ A = \begin{bmatrix} A_{11} & \cdots & A_{1J} \\ \vdots & & \vdots \\ A_{I1} & \cdots & A_{IJ} \end{bmatrix},\qquad B = \begin{bmatrix} B_{11} & \cdots & B_{1K} \\ \vdots & & \vdots \\ B_{J1} & \cdots & B_{JK} \end{bmatrix} $$ $$ AB = \begin{bmatrix} A_{11}B_{11}+\cdots+ A_{1J}B_{J1} & \cdots & A_{11}B_{1K}+\cdots+ A_{1J}B_{JK} \\ \vdots & & \vdots \\ A_{I1}B_{11}+\cdots+ A_{IJ}B_{J1} & \cdots & A_{I1}B_{1K}+\cdots+ A_{IJ}B_{JK} \end{bmatrix} $$ $$ AB = \begin{bmatrix} \sum_j A_{1j}B_{j1} & \cdots & \sum_j A_{1j}B_{jK} \\ \vdots & & \vdots \\ \sum_j A_{Ij}B_{j1} & \cdots & \sum_jA_{Ij}B_{jK} \end{bmatrix} $$ The inner blocks can be any dimensions as long as dimensions that need to match up are the same. For example \(A_{ij}\) and \(B_{jk}\) need to have matching inner dimensions (the \(j\) dimension) so that the multiplication \(A_{ij}B_{jk}\) makes sense.