Intuition: Coordinates
Given a set of vectors \(P_1,\dots,P_n \in \mathbb{R}^m \) organized as the columns of a matrix \(P \in \mathbb{R}^{ m \times n}\) $$ P = \begin{bmatrix} | & & | \\ P_1 & \cdots & P_n \\ | & & | \end{bmatrix} $$ we can represent other vectors as linear combinations of those vectors. This is illustrated in the basic figure shown. The vector \(y\) is a linear combination of the columns of \(P\) with coefficients \(x\), ie. \(y = Px\). Here, we say that \(x\) is the "coordinates of \(y\) with respect to the columns of \(P\)" (or just "with respect to \(P\)" for short.)
Once we've defined the new coordinate system \(x = Vx'\) that tells us how to represent \(x\) as a coordinates (\(x'\)) with respect to \(V\), if we now want to convert from the original \(x\)-coordinates to the \(x'\)-coordinates we actually need the inverse transformation.
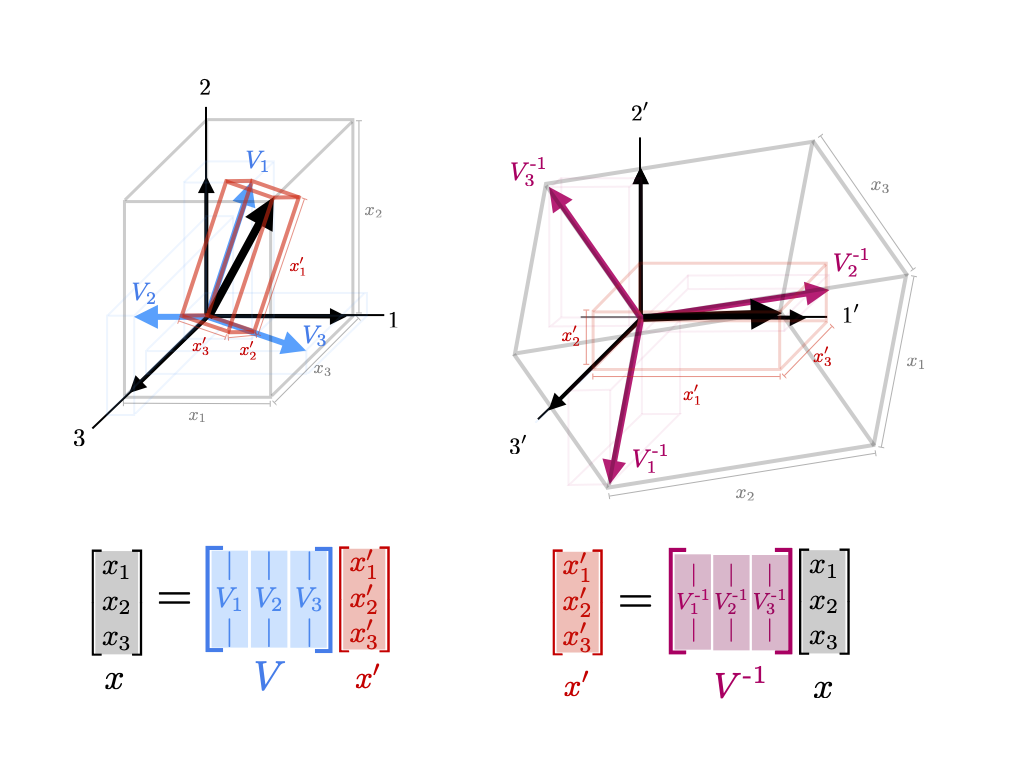
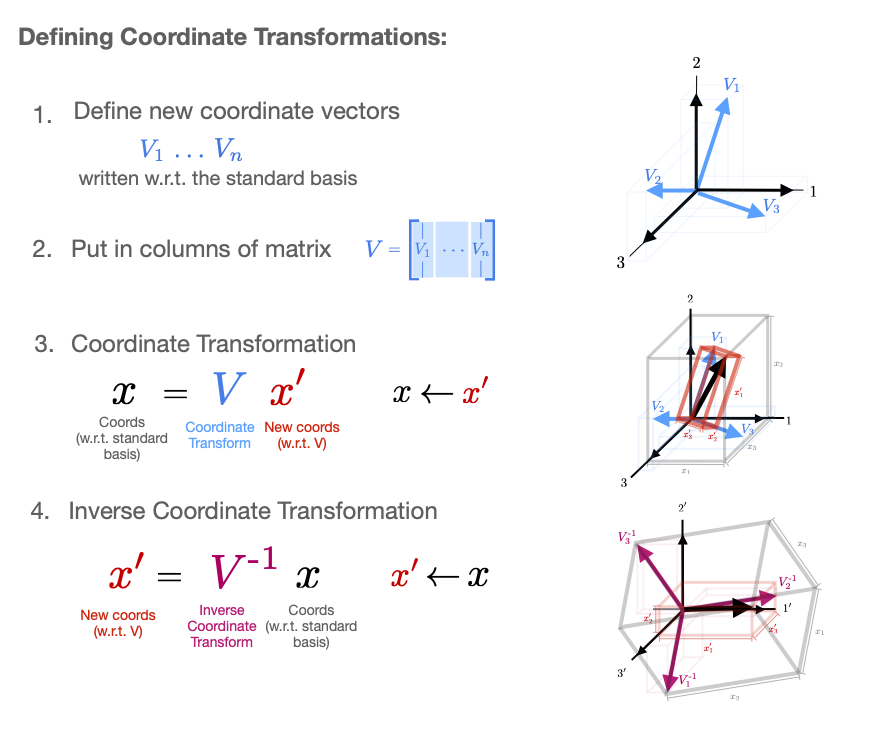
The process of defining a coordinate system is worth laying out in detail. If we have a vector \(x\) represented with respect to the standard basis and we want to represent it in terms of a new basis of vectors, the first step is to write those new basis vectors in terms of the standard basis. We then organize these basis vectors as the columns of a matrix \(V\) $$ V_1, \cdots, V_n \qquad \substack{w.r.t the \\ standard \\ basis} \qquad \Rightarrow \qquad \begin{bmatrix} | & & | \\ V_1 & \cdots & V_n \\ | & & | \end{bmatrix} $$ Conceptually, now it is clear that \(x'\) gives a linear combination of the columns of \(V\) (the new basis vectors) and that the equation \(x=Vx'\) says that \(x'\) is the representation of \(x\) in the new basis. We can also see that here both \(x\) and a the columns of \(V\) should be coordinates with respect to the same basis (the standard basis). If we know \(x'\) and want to convert \(x\), we simply compute \(x=Vx'\). If, however, we want to compute \(x'\) from \(x\), we need the equation \(x' = V^{-1}x\). We will discuss the details of the inverse operation next.