Vectors contain both the notion of length and direction. While magnitude is a property that vectors share with regular numbers, direction is a uniquely vector property. As such we can talk about the relative magnitude of two vectors and we can also talk about whether or not they point in similar directions, opposite directions or whether they are "perpendicular" or "orthogonal" to each other. The "inner product" or "dot product" of two vectors is at the heart of this direction comparison.
DefinitionThe inner product, denoted by \(\langle \cdot, \cdot \rangle\), between two vectors \(x, y \in \mathbb{R}^n\) is given by $$ \langle y,x \rangle = \sum_i y_ix_i $$ We can also write the inner product in several other ways. $$ \langle y,x \rangle = \sum_i y_ix_i = y^Tx = \lVert y \rVert_2 \lVert x \rVert_2 \cos(\theta) $$ The expression \(y^Tx\) uses matrix multiplication notation; \(y^T\) is a row vector and \(x\) as a column vector. (This expression is perhaps the most clean and useful algebraically.) The final expression \(\lVert y \rVert \lVert x \rVert_2 \cos(\theta)\) is the geometric definition of an inner product that we will consider more below. \(\lVert y \rVert_2\) and \(\lVert x \rVert_2\) are the magnitudes of \(x\) and \(y\) and \(\theta\) is the angle between the two vectors.
Geometry of Inner ProductsThe geometry of the inner product can be seen by considering the law of cosines (an extension of the Pythagorean theorem) detailed in the image below.
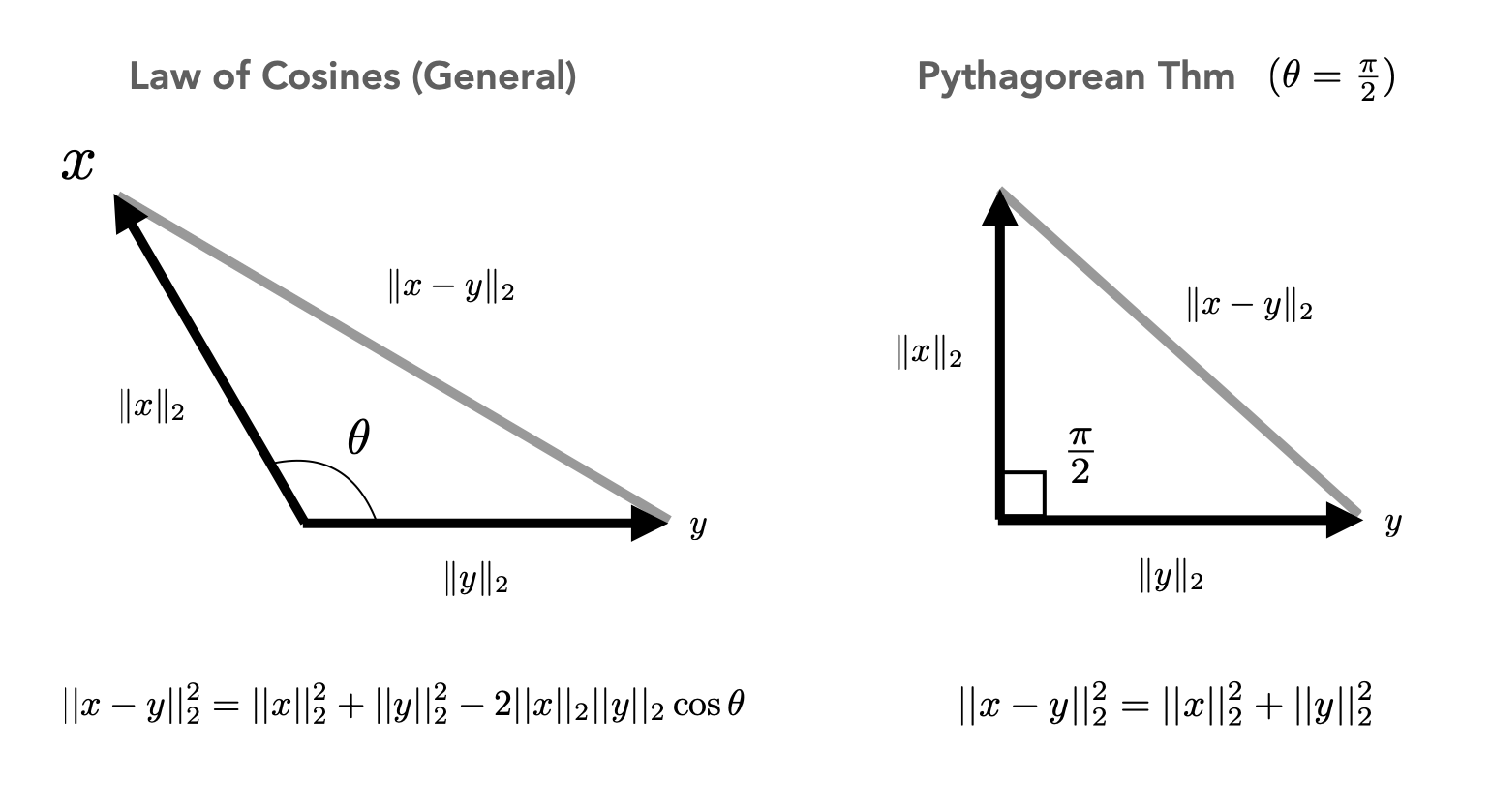
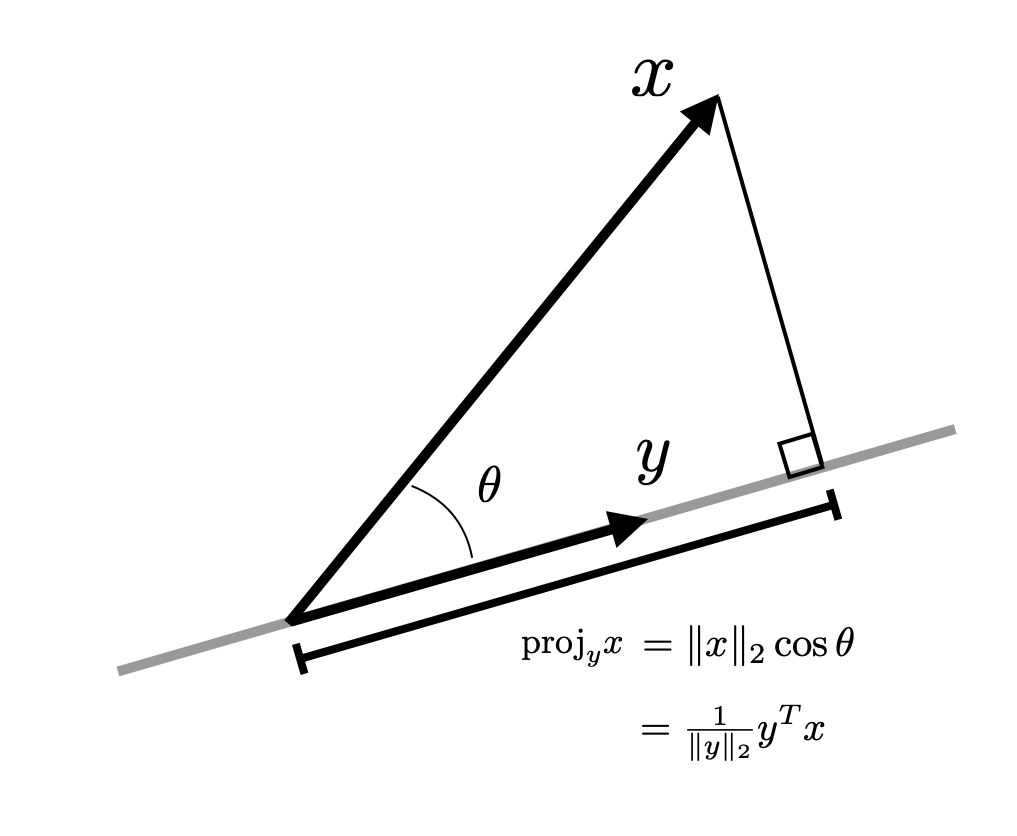
Note that the law of cosines is an extension of the Pythagorean theorem in that it gives a correction term for when \(\theta \neq \pi/2\). This correction term is closely related to the inner product between the vectors that form the sides of the triangle. Consider the norm (squared) of the vector difference \(x-y\) $$ (x-y)^T(x-y) = x^Tx + y^Ty - 2y^Tx $$ The law of cosines gives that the last term can be expressed as $$ 2y^Tx = 2 \lVert y \rVert_2 \lVert x \rVert_2 \cos(\theta) $$ which gives the geometric interpretation of the inner product. Note from this definition if two vectors \(x\) and \(y\) point in similar directions (small \(\theta\)) then \(y^Tx\) will be larger; if they are perpendicular (\(\theta=\pi/2\)) then \(y^Tx = 0\) and if they point in opposite directions (\(\theta\) closer to \(\pi\)) then \(y^Tx\) will be negative. The inner product is closely related to length of one vector after it is projected onto another. Specifically if \(y\) is a unit vector, then \(y^Tx\) is exactly the length of \(x\) after it is projected onto \(y\) as shown in the image below.
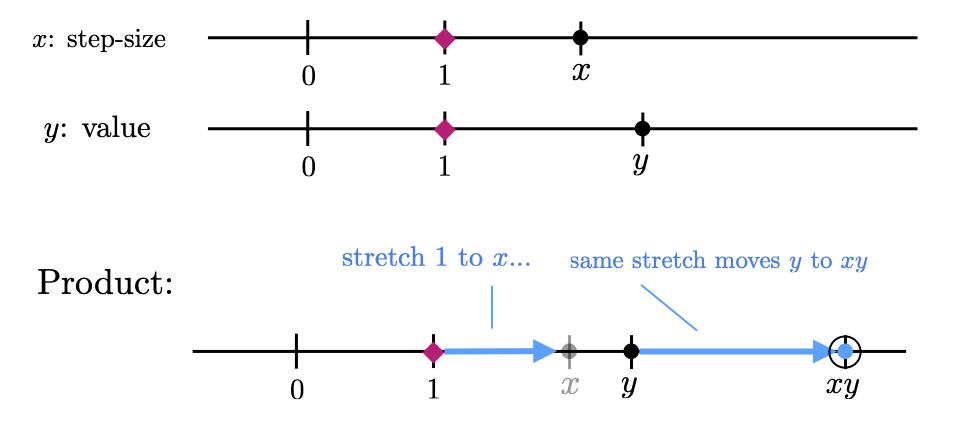
To better visualize the geometry of the inner product, we first consider scalar multiplication of two real numbers in the following way. For the product of any two real numbers \(x,y \in \mathbb{R}\), we can think of \(x\) as a step-size and \(y\) as how many steps we take (not necessarily an integer). On a number line, We can think of this as re-defining a unit for \(y\) as \(x\). Visually this is equivalent to dragging the value of 1 on the \(y\) number line to the value of \(x\) and allowing \(y\) to be stretched as well. As 1 goes to \(x\), \(y\) will go to \(xy\). If \(x\) is greater than 1, \(y\) gets stretched away from the origin; if \(x\) is less than one then \(y\) gets shrunk toward the origin. If the sign of \(x\) is negative then \(y\) also gets flipped to the otherside of the numberline. The value \(x=1\) is special in that it leaves \(y\) unchanged and \(x=-1\) leaves the magnitude of \(y\) unchanged but just flips the side of the numberline. We can illustrate this property in the figure below.
Unlike scalars, vectors contain both the notion of length and direction. If a scalar has some notion of direction it is simply a binary value \(\pm 1\), ie. is the number positive or negative. This "direction" determines whether or not multiplying by this number flips the direction of another number. Inner products can be thought of as expanding this binary value of \( \pm 1\) to a full \(360^o\) of relative orientation. Rather than simply flipping the sign of the vector product based on the directions of the vectors, inner product compares their relative direction and then multiplies by a number in the interval \([-1,1]\) given by \(\cos(\theta)\)
To adjust the visualization of scalar multiplication above to apply to inner products we first note that a unit step for \(y\) now includes a direction as well as a length. When taking the inner product rather than redefining the unit vector in the \(y\) direction as \(x\), we can find the vector in the \(y\) direction, \(v\), that would project to the unit vector in the \(x\) direction and redefine that vector as \(x\). If we let, \(y\) get stetched in the same way, the resulting length of the stretched \(y\) will be \(y^Tx\). This is visualized in the diagram below. Note that when we move \(v\) to \(x\), \(y\) moves along a parallel line.
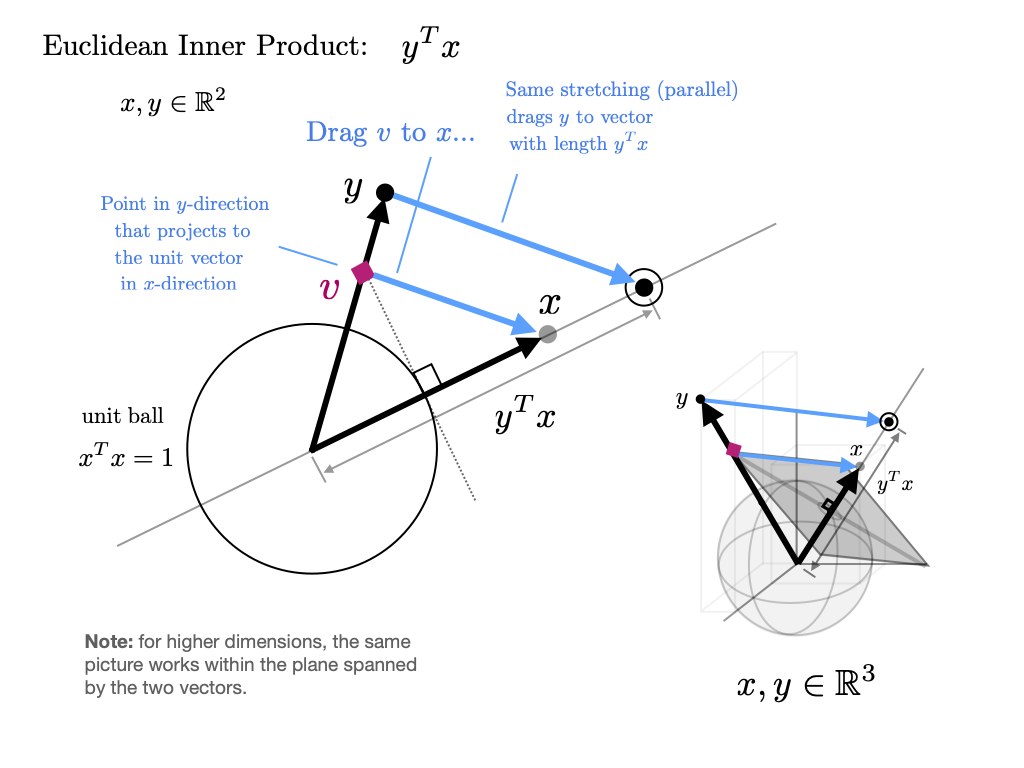
The vector \(v\) can be thought of as how far we have to go in the \(y\)-direction to get to one unit in the \(x\) direction. If \(x\) and \(y\) point in the same direction, then \(v\) just has length one (and this picture reduces to the scalar picture) but the more \(x\) and \(y\) point in different directions the larger the vector \(v\) gets, ie. the farther you have to go in the \(y\) direction to move one unit in the \(x\) direction. For large \(v\) the action of stretching \(v\) to \(x\) actually ends up shrinking \(y\) and so \(y^Tx\) becomes small. (The diagrams below are dense and worth considering slowly.)
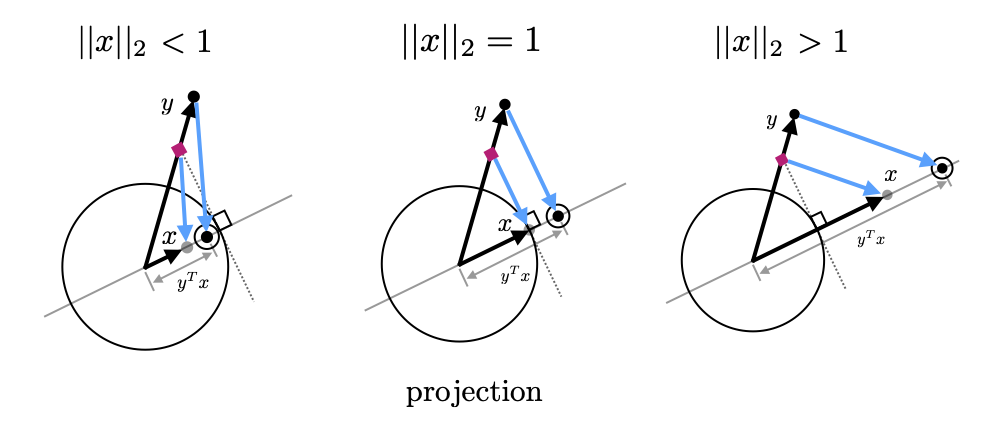
Several other special cases are worthy of note. If \(x\) is just a unit vector this operation ends up just giving the length of \(y\) projected onto the direction of \(x\). This idea of projection is at the heart of the difference between inner products and scalar products. Scalar products just scale the magnitude of the thing they multiply; inner products both scale and project the things they multiply. Another special case is when \(y\) and \(x\) are perpendicular. Here the visualization above reaches a limiting case where the vector \(v\) shoots off to infinite. Dragging \(v\) to \(x\) then shrinks \(y\) to 0. Intuitively since \(y\) does not point in the direction of \(x\) at all, we have to go out to infinite to move one unit in the \(x\) direction.
The algebra of this visualization is the following. \(v\) is the vector in the \(y\)-direction such that \(v^T\tfrac{x}{\lVert x\rVert_2} = \lVert v\rVert|_2 \cos \theta = 1\). Since \(v\) and \(y\) point in the same direction, we can define \(y = \beta v\), ie. \(y\) is just a scaled version of \(v\). We then get that $$ y^Tx = \beta v^T \tfrac{x}{\lVert x \rVert_2} \lVert x \rVert_2 = \beta \lVert x\rVert_2 $$ ie. the same scaling (\(\beta\)) that scales \(v\) to \(y\) also scales \(x\) to a vector with length \(y^Tx\). The geometric interpretation above is just this visualized using similar triangles.
Note: this section is better understood with background in positive definite matrices.
We can generalize the Euclidean inner product with a positive definite symmetric matrix \(P \succ 0\), \(P=P^T \in \mathbb{R}^{n \times n}\) to get the \(P\)-inner product defined as $$ \langle y,x \rangle_P = \Vert x \Vert_P = y^TPx $$ Rather than a uniform, spherical geometry, this inner product induces an ellipsoidal geometry. One interpretation of this inner product is that each vector \(x\) and \(y\) is transformed (stretched) using the coordinate transfromations \(x' = P^{\tfrac{1}{2}}x\) and \(y'=P^{\tfrac{1}{2}}y\) before the regular Euclidean inner product is applied. The unit ball \(x^TPx = 1\) is ellipsoidal rather than spherical in the \(x\)-coordinates (but it is spherical in the \(x'\)-coordinates). A projection in this ellipsoidal geometry does not follow perpendicular lines but rather lines tangent to the unit ball. Since the ellipsoid changes based on direction, the directions of projection change with direction as well. The visualization of the inner product given above is similar but now the unit vector in the \(x\)-direction is shown by the ellisoid and \(v\) is the intersection of the \(y\)-direction and the tangent space to the ellipsoid where \(x\) crosses it. This new geometry is illustrated in the diagram below.
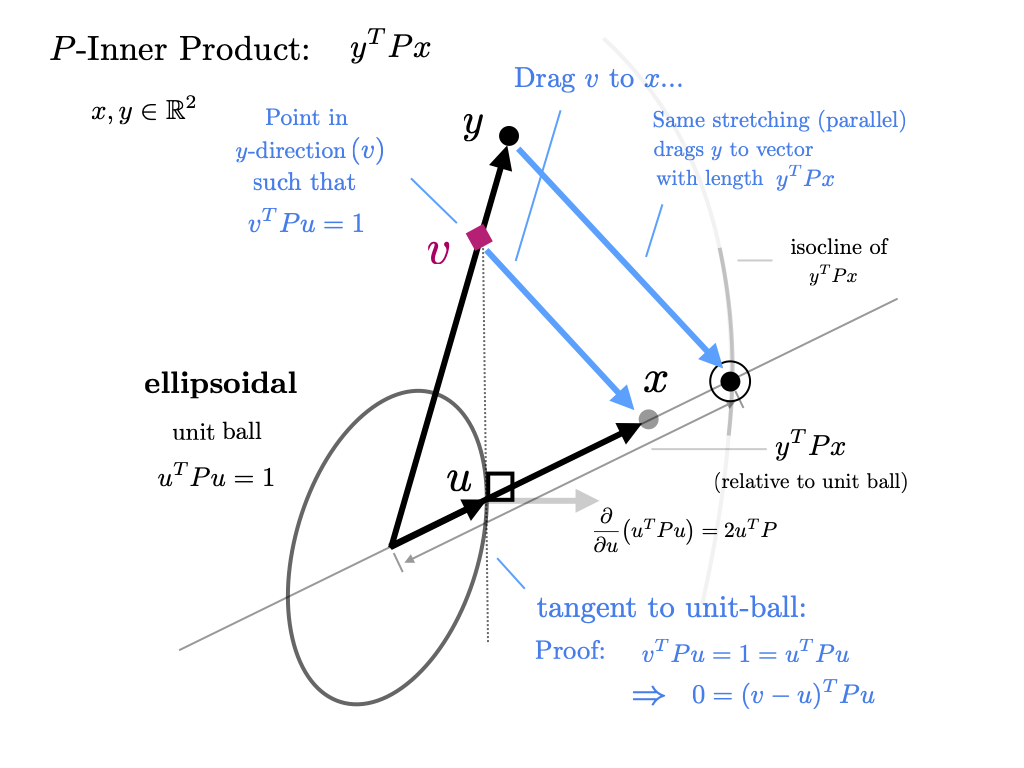
Note that for the \(P\)-inner product, orthogonality, ie. \(y^TPx= 0\), does not imply that the angle between the two vectors is \(90^o\). Graphically, orthogonality is better understood as one vector being parallel to a tangent vector where the other vector crosses the unit ball. This is illustrated below and discussed more in the section on orthogonality.
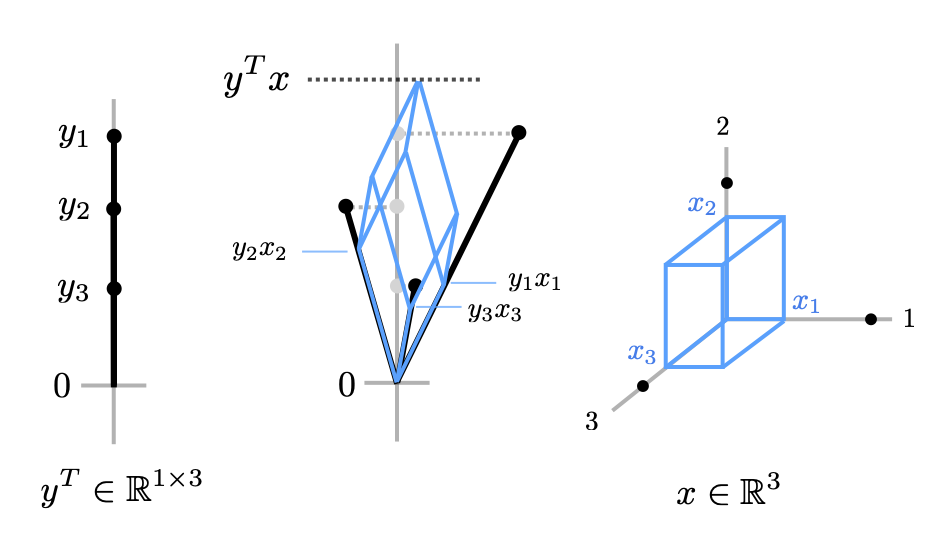
Another perspective on the inner product \(y^Tx\) (perhaps closer to the notion of matrix multiplication) is to think of the row vector \(y^T\) as a set of columns (each of length) one and then \(x\) as a set of coordinates. We can then visualize the inner product in the following way.