INVERSES

Basics

We say $P$ is invertible if there is a unique $x'$ that solves $x=Px'$ for any $x \in \mathbb{R}^n $, ie. if the columns of $P$ form a basis for $\mathbb{R}^n$.

There are many characteristics of a matrix that are equivalent to invertibility. At the end of this page we give a detailed list of these characteristics. There are also many ways to compute inverses using Gaussian Elimination, Householder transformations, etc. We will cover these later. Initially, we focus on intuition for inverses.

The inverse of an invertible (square) matrix $P$ is the unique matrix square matrix such that $$ PP^{-1} = P^{-1}P = I $$ If a matrix is invertible than any two vectors $x,x' \in \mathbb{R}^n$ that satisfy $x = Px'$ can be thought of as equally valid representations of any given vector; $x$ is the coordinates of that vector with respect to the standard basis and $x'$ is the coordinates with respect to the columns of $P$. We can transform back and forth between the two representations using the inverse. Left multiplying $x=Px'$ by $P^{-1}$ gives $$ P^{-1}x = P^{-1}Px' \quad \Rightarrow \quad x' = P^{-1}x $$ Left multiplying $x' = P^{-1}x$ by $P$ tranforms back. $$ Px' = PP^{-1}x \quad \Rightarrow \quad x = Px' $$ If we represent a vector $x$ in terms of two different bases other than the standard basis (let's say $P$ and $Q$), then we can get two alternate set of coordinates ($x'$ and $x''$) such that $x = Px'$ and $x = Qx''$. The relationship between $x'$ and $x''$ can the be computed by using the equation $$ Px' = x = Qx'' \qquad \Rightarrow \qquad x' = P^{-1}Qx'' \quad and \quad x'' = Q^{-1}Px' $$ While perhaps pedantic, writing this out explicitly is worth doing since it is a very common construction used in practice. We often want to define two arbitrary coordinate systems $P$ and $Q$ in the same space and then convert in between them.

Side Note: Left and Right Inverses

Side note: It is also possible to have situations where we can only find a $P^{-1}$ to satisfy either only $P^{-1}P=I$ or $PP^{-1} = I$ but not the other. If there exists $P^{\ell}$ such that $P^{\ell}P = I$ we say that $P$ is left-invertible and $P^{\ell}$ is the left inverse. If there exists $P^{r}$ such that $PP^{r} = I$ we say that $P$ is right-invertible and $P^{r}$ is the right inverse. We will cover the situations where $P$ is only right or left-invertible later (since they are significantly more complicated - $P$ need not even be square,etc). For now we will simply note that if both a right and left-inverse exist for a matrix $P$ then they are the same matrix $P^{\ell} = P^{r} = P^{-1}$. This fact comes from considering the product $P^\ell P P^r$ using the (very basic) associative property of matrix multiplication. $$ P^{\ell} = P^\ell P P^r = P^{r} $$ The first equality comes from considering the product $P \cdot P^r = I$ in the center expression first; the second equality comes from considering the product $P^\ell \cdot P=I$ first.

Inverse Intuition

We first start by giving an intuitive picture of the action of matrix $P^{-1}$. The equation $x = Px'$ tells us that the coordinates of $x$ with respect the columns of $P$ are given by $x'$. In the low dimensional case if we know $x$ we can see what $x'$ is going to be fairly easily for any given $x$ by looking at how we would have to move along each column of $P$ to get to $x$. We can also see that if $P$ forms a basis for the space (spans the whole space and is linearly independent) then there will be a unique $x'$ for any $x$. $P^{-1}$ is the matrix transformation that precisely gives us $x'$ for any $x$. We can visualize it's action in the following way. Consider having $n$-hands,one for each column of $P$. Now consider grabbing each column of $P$ and all at once pulling the first column of $P$ to the first standard basis vector $I_1$, pulling the second column of $P$ to the second standard basis vector $I_2$, etc. Now picture the overall space as being stuck to the columns of $P$ and moving with your hands as you pull. The point $x$ in the space moves with the whole space as you pull it. When each column of $P$ reaches the appropriate standard basis $x$ has moved as well; this new locatin of $x$ is $x'$ and the action you just performed is the transformation $P^{-1}$. Mathematically, this is a description of the equation of the equation $P^{-1}x = P^{-1}Px' = x'$. We can see this better if we write it out in more detail. $$ P^{-1}x = P^{-1}Px' = P^{-1} \begin{bmatrix} | & & | \\ P_1 & \cdots & P_n \\ | & & | \end{bmatrix} x' = \begin{bmatrix} | & & | \\ P^{-1}P_1 & \cdots & P^{-1}P_n \\ | & & | \end{bmatrix} = \begin{bmatrix} 1 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & 1 \end{bmatrix} x' = x' $$ ie. $P^{-1}$ moves each column of $P$ to the corresponding standard basis vector and in so doing moves $x$ to $x'$. This process for $P \in \mathbb{R}^{2 \times 2}$ and $P \in \mathbb{R}^{3 \times 3}$ is illustrated in the figures below.

We note that if we draw a vector $x$ as coordinates with respect to the columns of $A$, we get $y=Ax$. The same action of the matrix inverse moves the vector $y$ to $x$. We can illustrate this similarly to the visualization above but with $x$ and $y$ drawn also.

We now pull apart the two equations $$ P^{-1}P = PP^{-1} = I $$ from the perspective of the column and row geometry of both $P$ and $P^{-1}$. As noted in the matrix multiplication we can think of any matrix product $AB$ from four perspectives with $A$ and/or $B$ as columns and/or rows. We consider products $P^{-1}P$ and $PP^{-1}$ from each of these perspectives and thus we get 8 different perspectives to consider. For each geometry (column-column, row-column, etc) we present analysis of both products together and discuss their relationship. One or another geometry/perspective maybe useful depending on the application. None are simple but some are more straightforward than others. They are subtly similar and different so one may not want to digest them all at once. We give a difficulty score for each to help any new students of linear algebra focus their efforts.

Matrix-Column Geometry (Difficulty: 1/10)

The picture shared above is a visualization of the matrix-column geometry of the equation $P^{-1}P = I$, ie. multiplying each column of $P$ by $P^{-1}$ transforms them to the appropriate standard basis vectors. Similarly, the equation $PP^{-1}=I$ gives that $P$ transforms the columns of $P^{-1}$ to the standard basis vectors well. In order to visualize this relationship, we start with $P$ and then visualize left multiplication by the sequence of matrices $$ P^{-1} \quad \Rightarrow \quad P^{-1} \quad \Rightarrow \quad P \quad \Rightarrow P \quad P^{-1} \quad P^{-1} $$ This sequence causes the product to fluctuate back and form between $P$, $I$, $P^{-1}$, $I$, $P$, etc to visualize how each transformation works. The fundamental matrix property that both $PP^{-1}=I$ and $P^{-1}P = I$ can be restated as "the same transformation that moves $P$ to the identity is also moved to the identity by $P$".

Column-Column Geometry (Difficulty: 1/10)

The column-column geometry of $P^{-1}P$ and $PP^{-1} $ is perhaps the most straightforward and intuitive. From the equation $PP^{-1} = I$ we see that the columns of $P^{-1}$ are the coordinates of each of the standard basis vectors with respect to the basis $P$. More explicitly The inverse of $P$ is the matrix $P^{-1}$ such that $PP^{-1} = I $ Expanding this equation we have that $$ I = PP^{-1} = \Bigg[ \ \ P \ \ \Bigg] \begin{bmatrix} | & & | \\ Q_1 & \cdots & Q_n \\ | & & | \end{bmatrix} = \begin{bmatrix} | & & | \\ PQ_1 & \cdots & PQ_n \\ | & & | \end{bmatrix} $$ Thus, $Q_i$, the $i$th column of $P^{-1}$ is the coordinates of the $i$th standard basis vector with respect to the columns of P. We illustrate this in the image below.

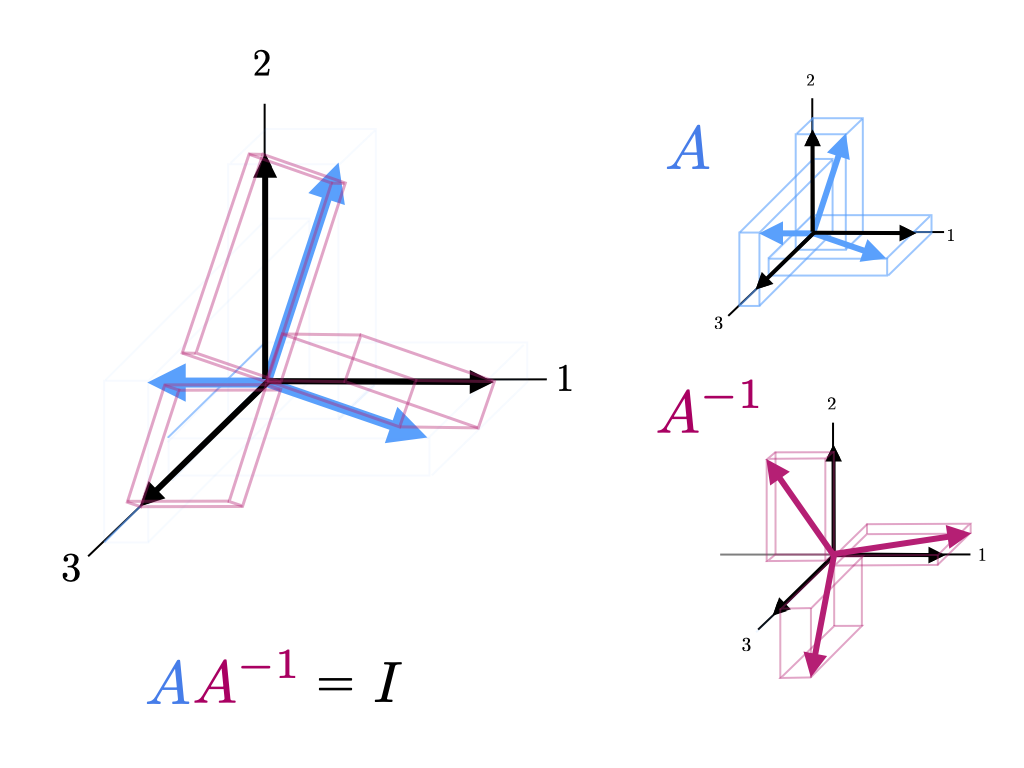
Similarly, the columns of $P$ are the coordinates of the standard basis vectors with respect to $P^{-1}$. The fact that the coordinates of $I$ with respect to the basis $P$ (ie. $PP^{-1}=I$) form basis for which $P$ are the coordinates of $I$ is perhaps a deep fact.

Row-Matrix and Row-Row Geometry (Difficult: 1/10)

As discussed in the matrix product section, the row-matrix and row-row geometry in general is quite similar to the matrix-column and column-column geometry with rows replacing columns conceptually and the direction of multiplication reversed. We reproduce the first picture from the previous section with rows instead of columns for eye-candy and leave it at that.

Row-Column Geometry (Difficulty: 3/10)

The study of matrix inverses is one of the primary places where the row-column geometry bears quite interesting fruit. In summary, the row-column geometry of $P^{-1}P=I$ indicates that each row of $P^{-1}$ has inner product 1 with the corresponding column of $P$ and (perhaps more fundamentally) is orthogonal to every other column of $P$. (Similarly, the row-column geometry of $PP^{-1}$ indicates that each row of $P$ has inner product 1 with the corresponding column of $P^{-1}$ and is orthogonal to every other column of $P^{-1}$. This perspective is actually quite fruitful. For example, if we want to know the direction of the first column of $P^{-1}$ we can look at the span of rows 2 thru $n$ and compute the orthogonal direction. If we then want to know the length of that first column of $P$, we look at the inner product of that direction with the first row of $P$. We could continue with a similar procedure for every column of $P^{-1}$. This geometry is illustrated in the figure below. This is not at all an efficient way to compute an inverse of matrix but it allows us to compute parts of a matrix individually without computing the whole. The geometry is also the fundamental idea behind Cramer's determinant rule, a quite old and deep fact about systems of equations. It is also fundamental in helping us understand when and how the invertibility of a matrix breaks down. We expound on this more in the section on degrees of matrix invertibility and matrix condition number.

The above geometry is illustrated in the figures below.

Column-Row Geometry (Difficulty: 7/10)

As mentioned in the matrix product discussion, this last perspective is the most esoteric. Below we show this outer product sum for $A$ times $A^{-1}$.

and then for $A^{-1}$ times $A$.