A linear combination of a set of vectors \(\big\{A_1,\dots,A_n\big\}\) is weighted sum of those vectors $$ A_1 x_1 + A_2 x_2 + \cdots + A_n x_n $$ where the weights or coefficients are scalars \(x_1,\dots,x_n \in \mathbb{R}\). Basic linear combinations of one, two, three, and four vectors are shown below.

The set of all possible linear combinations is called the span of a set of vectors. Spans of one,two, and three vectors are shown in the image below. Note that spatially The span of a set of vectors forms a hyperplane or subspace that passes through the origin and extends out in any directions the vectors point. Since negative coefficients are possible the span also extends in the opposite direction of the vectors. If we add a new vector to the set of vectors that does not already lie in the span of the original vectors then we increase the dimension of the spanned subspace. If we add a new vector that was already in the span, the dimension of the spanned subspace does not increase
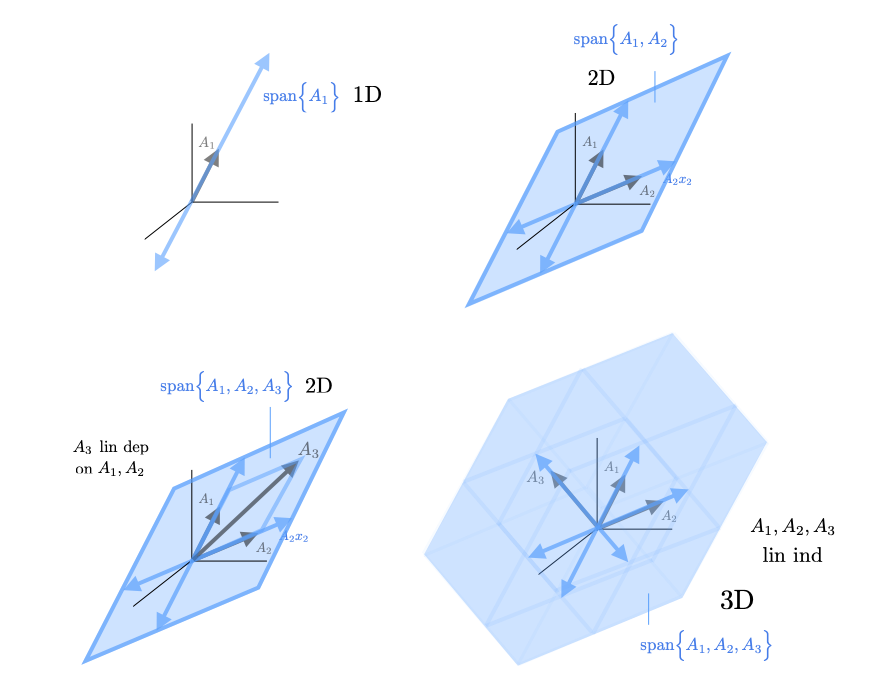
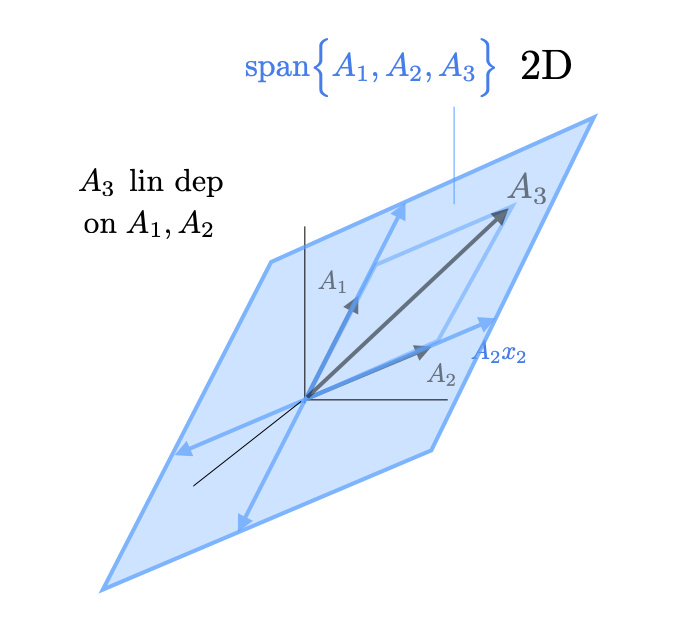
We say a vector is linearly dependent on a set of vectors if it lies in the span of those vectors, ie. one can construct that vector as a linear combination of vectors in the set. Algebraically, \(y\) is linearly dependent on a set of vectors \(\big\{A_1,\dots,A_n\big\}\), we can find coefficients \(x_1,\dots,x_n \in \mathbb{R}\) such that $$ y = A_1 x_1 + \cdots + A_n x_n $$ If a vector is not linearly dependent on a set of vectors, we say it is linearly independent from that set. We say a set of vectors is linearly independent if none of the vectors are linearly dependent on the other vectors in the set, and we say the set is linear dependent if any of the vectors are linearly dependent on the others. The image below shows the case where a vector \(A_3\) is linearly dependent on vectors \(A_1,A_2 \in \mathbb{R}^3\).
This next section discusses linear dependence and independence in rigorous mathematical terms. A student of linear algebra will quickly note that understanding/working with these definitions can actually be a lot more difficult than understanding the concepts given above. While one should not shy away from the rigorous math, one should also keep in mind the simple intuition for the concepts given above.
A compact way to state mathematically that a set of vectors \(\big\{A_1,\dots,A_n\big\}\) is linearly dependent is to say, there exists a vector of coefficients \(x \neq 0\) such that $$ A_1 x_1 + \cdots + A_n x_n = 0 $$ This statement encodes that there is at least one vector \(A_i\) that is dependent on the others. Here, \(x \neq 0\) means that at least one of the coefficients is not equal to 0. Since at least one \(x_i\) is nonzero (assume it is \(i=1\) for simplicity), we can write $$ A_1x_1 = -A_2 x_2 - \cdots -A_n x_n $$ We can then explicitly write \(A_1\) as a linear combination of the others $$ A_1 = A_2\left(- \tfrac{x_2}{x_1}\right) + \cdots + A_n\left(- \tfrac{x_n}{x_1}\right) $$ Note: if all the other \(x_i\)'s are zero, then \(A_1\) must be the zero vector which is linear dependent on any set of vectors.
Negating the above statement gives a mathematical definition of linear independence. A set of vectors \(\big\{A_1,\dots,A_n\big\}\) is linearly independent if there does not exist a nonzero vector \(x\) such that \(A_1x_1+\cdots + A_n x_n = 0 \). We can rephrase this in several ways: a set is linearly independent if \(A_1x_1+\cdots + A_n x_n = 0 \) only when \(x=0\) or a set of vectors \(\big\{A_1,\dots,A_n\big\}\) is linearly independent if $$ A_1x_1+\cdots + A_n x_n = 0 \qquad \Rightarrow \qquad x = 0 $$ This last characterization is by far the most useful in mathematical proofs. If we can show that the sum condition on the left implies \(x=0\) then we know the set of vectors is linearly independent.
More Math: Proving Linear Independence (Difficulty: 3/10)These next comments assume an understanding of matrix multiplication and matrix column geometry.
Practically when we try to prove linear independence (or dependence) of a set of vectors (say \(n\) vectors each in \(\mathbb{R}^m\)), we often write them as columns of a matrix \(A \in \mathbb{R}^{m \times n}\) and write vector of coefficients as \(x \in \mathbb{R}^n\). The linear dependence condition becomes there exist \(x \neq 0\) such that \(Ax = 0\), ie. \(A\) has a nontrivial right nullspace. The linear independence condition becomes \(Ax=0 \Rightarrow x =0 \). This is quite compact and useful. For example, suppose \(A\) can be divided into rows \(A'\) and \(A''\) where we already know that \(A'\) has linearly independent columns. We can then show immediately that \(A\) must have linearly independent columns as well $$ Ax = \begin{bmatrix} A' \\ A'' \end{bmatrix} x = \begin{bmatrix} A'x \\ A''x \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$ Since \(A'x=0\) then \(x=0\) (by the linear independence of the columns of \(A'\)) and thus we have shown that \(Ax=0\) implies \(x = 0\) as desired. This often arises in the even simpler context where \(A'\) is just the identity matrix. In this case we simply have $$ Ax = \begin{bmatrix} I \\ A'' \end{bmatrix} x = \begin{bmatrix} x \\ A''x \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \qquad \Rightarrow \qquad x = 0 $$ We will return to this construction in our construction of bases for range and nullspaces.