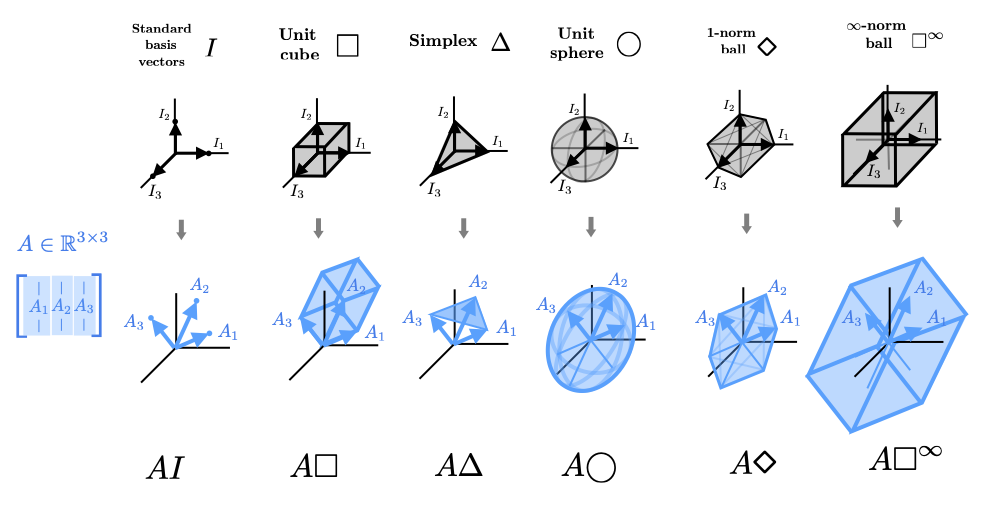
Intuitively, a linear transformation on a space is some combination of stretching, skewing, rotation, and reflection. Intuition for the action of these transformations is perhaps best given by visualizing how various shapes and sets transform under linear transformations. As previously mentioned, each column of \(A\) tells where a standard basis vector in the original vector space is mapped to in the transformed space. For example, the second standard basis vector, \(I_2\), maps to the 2nd column, etc. $$ \begin{bmatrix} | & | & & | \\ A_1 & A_2 & \cdots & A_n \\ | & | & & | \\ \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} = \begin{bmatrix} | \\ A_2 \\ | \end{bmatrix} $$ If we draw the columns of the matrix as vectors (in the co-domain), we can see how the space transforms. We start out by giving several interactive examples of \(2 \times 2\) and \(3 \times 3\) transformations to give a better flavor for how the space is distorted and stretched. Note particularly the grid-lines in 2D. Note also that these are just a few examples and are by no means meant to be exhaustive. The space of potential \(m \times n\) matrices is as rich as there are ways to draw \(n\) different column vectors in an \(m\) dimensional space.
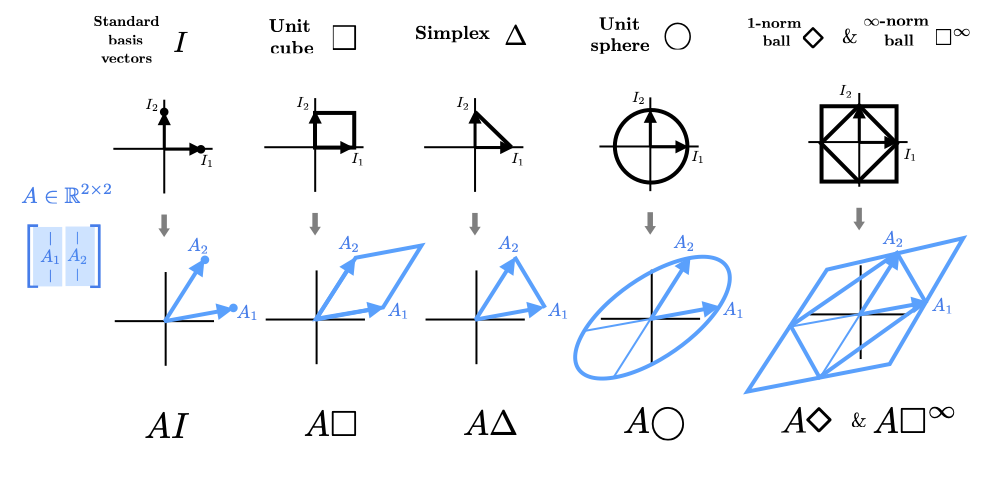
and \(3 \times 3\) square matrices. In both these cases, the domain and co-domain have the same dimension and we can think of the transformation as happening on the domain directly.
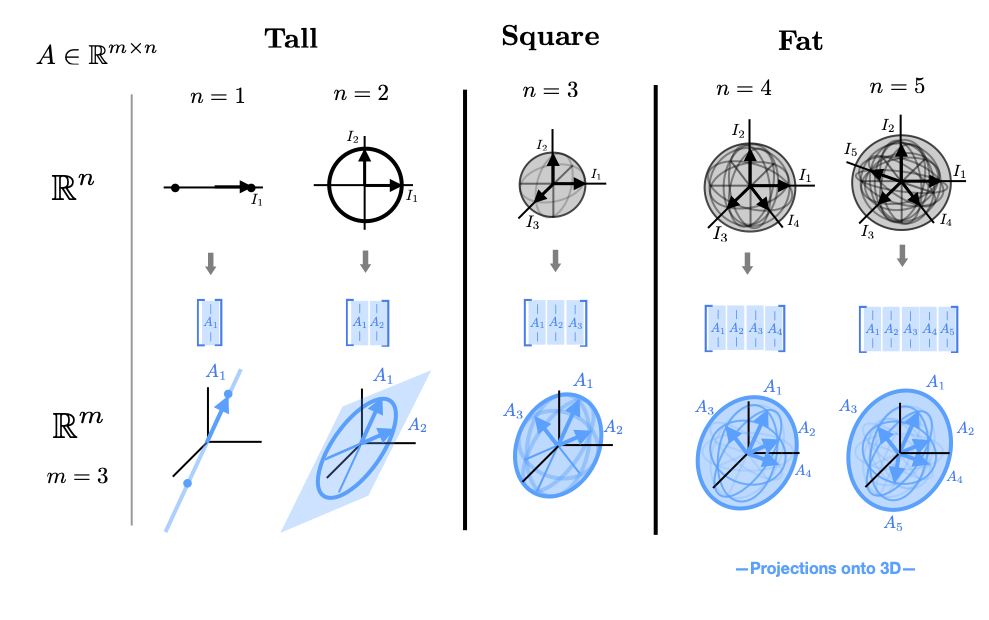
If the row and column dimension of \(A\) are different than the input and output spaces have different dimensions. If \(A\) is a fat higher dimensional sets are projected down onto a lower dimensional space. If \(A\) is tall than a lower dimension set is projected onto a subspace of the higher dimensional co-domain (given by the span of the columns of \(A\). We illustrate this for several cases when \(A\) is fat and several when \(A\) is tall below.
There are many types of intuitive transformations that are in fact linear. We will discuss the technical definition of a linear transformation later; but we can give an intuitive (and quite circular) definition now. A linear transformation is any transformation that can be represented by a matrix in the sense discussed above. In particular, a linear transformation is one that if we define where the axes transform to (ie. the columns of the matrix), we can see how the rest of the space moves by picturing it as getting "dragged along" with this motion.
Algebraically, this is closely related to the fact that matrix multiplication is distributive. If we represent a vector \(x \in \mathbb{R}^n \) as a sum of scaled standard basis vectors. $$ x = I_1 x_1 + \cdots + I_n x_n $$ we then have that \(Ax\) is given by $$ Ax = AI_1x_1 + \cdots + AI_nx_n = A_1 x_1 + \cdots + A_n x_n $$ This distributive property is the heart of the idea of linearity. We will give more thorough technical definitions later.
Linear transformations includes many intuitive transformations: stretchings, reflections, skewings, rotations, and combinations of these. We show several illlustrative examples of these different types of transformations below in 2D and 3D. Again, these examples are not meant to be exhaustive but to give a flavor. It is quite to useful to be able to picture a linear transformation (based on the columns of it's representing matrix) and mentally break it down into various combinations of these simpler intuitive transformations. This can be done in several more precise ways using matrix decompositions: QR decomposition, singular value decomposition, and most importantly eigenvalue decompositions. We will discuss this later.

Finally, we include an interactive visualization of how a matrix transforms sets and points that we will discuss more later.