.dcmath - UNDER CONSTRUCTION

A matrix \(A \in \mathbb{R}^{m \times n}\) is a block of numbers of the form $$ A = \begin{bmatrix} A_{11} & \cdots & A_{1n} \\ \vdots & & \vdots \\ A_{m1} & \cdots & A_{mn} \end{bmatrix} = \begin{bmatrix} | & & | \\ A_{1} & \cdots & A_n \\ | & & | \end{bmatrix} $$ There are many useful perspectives on matrices and matrix algebra but perhaps the most basic is that a matrix is a collection of column vectors as indicated above. Here we have \(n\) column vectors each of dimension \(m\), \(A_i \in \mathbb{R}^m \). Multiplication of a matrix \(A \in \mathbb{R}^{m \times n}\) times a vector \(x \in \mathbb{R}^n \) is designed to represent taking linear combinations of the columns of \(A\) with coefficients give by \(x\). $$ Ax = \begin{bmatrix} | & & | \\ A_{1} & \cdots & A_n \\ | & & | \end{bmatrix} \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} | \\ A_{1} \\ | \end{bmatrix} x_1 + \cdots + \begin{bmatrix} | \\ A_n \\ | \end{bmatrix} x_n $$ A matrix \( A \) is used to represent a linear transformation from one vector space another. Each column of \(A\) tells where a standard basis vector in the original vector space (called the domain) gets mapped to in the transformed vector space (the co-domain). For example, $$ \begin{bmatrix} | & | & & | \\ A_1 & A_2 & \cdots & A_n \\ | & | & & | \\ \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} = \begin{bmatrix} | \\ A_2 \\ | \end{bmatrix} $$

In the next section, we will discuss further how matrices represent linear transformations but we first give an interactive illustration of how a vector \(x\) is transformed by a matrix \(A\) based on the columns of \(A\).

Expressing the above multiplication \(Ax\) in terms of the individual elements of \(A\) we get $$ Ax = \begin{bmatrix} A_{11} & \cdots & A_{1n} \\ \vdots & & \vdots \\ A_{m1} & \cdots & A_{mn} \end{bmatrix} \begin{bmatrix} x_{11} \\ \vdots \\ x_{n1} \end{bmatrix} = \begin{bmatrix} A_{11}x_1 + \cdots + A_{1n}x_n \\ \vdots \\ A_{m1}x_1 + \cdots + A_{mn}x_n \end{bmatrix} $$ If we replace \(x\) with a full matrix \(B \in \mathbb{R}^{n \times p}\), we treat each column of \(B\) as a separate set of coefficients. $$ AB = \begin{bmatrix} | & & | \\ A_{1} & \cdots & A_n \\ | & & | \end{bmatrix} \begin{bmatrix} B_{11} & \cdots & B_{1p} \\ \vdots & & \vdots \\ B_{n1} & \cdots & B_{np} \end{bmatrix} = \begin{bmatrix} | & & | \\ A_1 B_{11} + \cdots + A_n B_{n1} & \cdots & A_1 B_{1p} + \cdots + A_n B_{np} \\ | & & | \end{bmatrix} $$ Again, expressed in terms of \(A\) and \(B\)'s individual elements this multiplication is given by $$ AB = \begin{bmatrix} A_{11} & \cdots & A_{1n} \\ \vdots & & \vdots \\ A_{m1} & \cdots & A_{mn} \end{bmatrix} \begin{bmatrix} B_{11} & \cdots & B_{1n} \\ \vdots & & \vdots \\ B_{m1} & \cdots & B_{mn} \end{bmatrix} $$ $$ = \begin{bmatrix} A_{11}B_{11}+ \cdots + A_{1n}B_{n1} & \cdots & A_{11}B_{1p}+ \cdots + A_{1n}B_{np}\\ \vdots & & \vdots \\ A_{m1}B_{11}+ \cdots + A_{mn}B_{n1} & \cdots & A_{m1}B_{1p}+ \cdots + A_{mn}B_{np} \end{bmatrix} $$ Note that for this multiplication to make sense the "inner" dimensions of \(A\) and \(B\) must match, ie. to multiply \(A \in \mathbb{R}^{m \times n}\) and \(B \in \mathbb{R}^{o \times p}\) we must have \( n = o \).

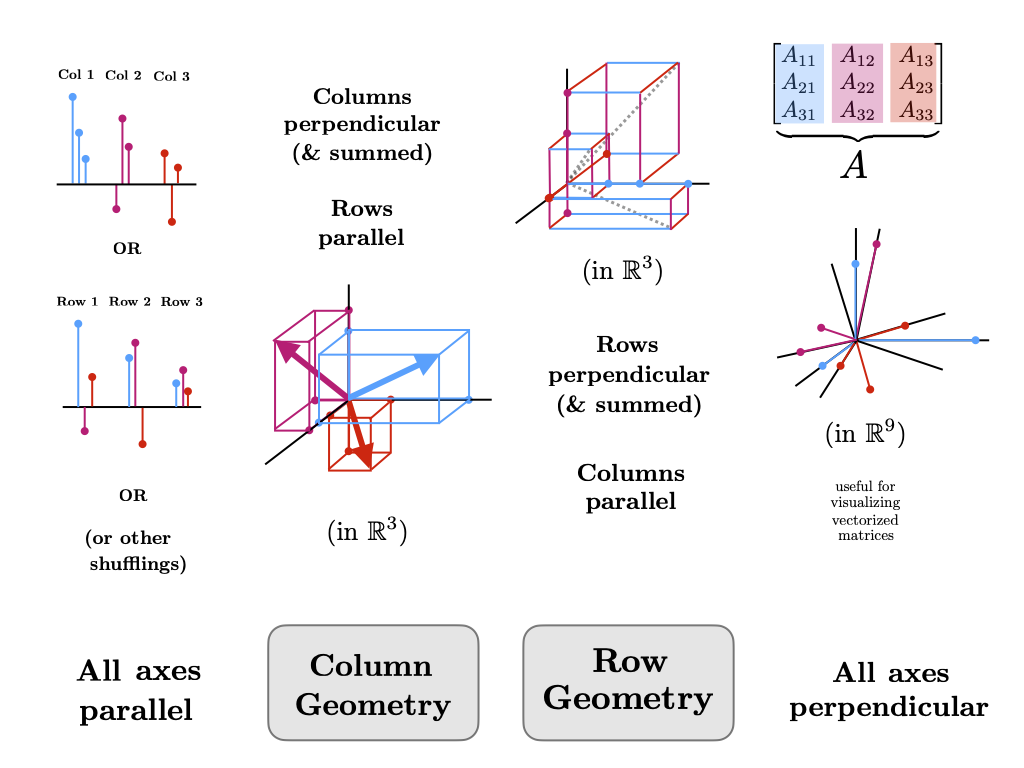
Note above we have assumed each element \(A_{ij}\) and \(B_{jk}\) are individual scalars. However, this form can make sense as well when \(A_{ij}\) and \(B_{jk}\)are each submatrices. This is VERY important practically for doing matrix algebra and is expounded in much more detail in the section on block matrix structures. For now, we note that to use this block matrix form, each subblock \(A_{ij}\) must have the same number of columns as \(B_{jk}\) has rows and the resulting terms in the product will be made up of subblocks as well.

Matrix multiplication by scalars is done the same as vectors; each element is scaled by the scalar.

Matrix addition (and subtraction) are done element-wise like vectors as well.