MATRIX MULTIPLICATION

When we multiply two matrices $A$ and $B$ together $AB$ we can think of $A$ as acting on each of the columns of $B$ separately $$ AB = \Bigg[\ \ A \ \ \Bigg] \begin{bmatrix} | & & | \\ B_1 & \cdots & B_n \\ | & & | \\ \end{bmatrix} = \begin{bmatrix} | & & | \\ AB_1 & \cdots & AB_n \\ | & & | \\ \end{bmatrix} $$ The basis for our intuition for matrix-matrix multiplication is thus the same as our intuition for matrix-vector multiplication

Primary Perspectives

There are many fruitful perspectives on the geometry of matrix multiplication. We list several of them here. Depending on the context one or another may be most fruitful. We note also that algebraically these perspectives are represented in various interesting cases of block matrix multiplication. (See the block matrix multiplication section.) We start out by listing perhaps the two most natural perspectives one for left-multiplication, the other for right multiplication.

Matrix-Column: Left-multiplication

When left-multiplying $B$ by a matrix $A$ perhaps the most natural perspective is to think of $A$ transforming each column of $B$ separately. $$ AB = \Big[ \ A \ \Big] \begin{bmatrix} | & & | \\ B_1 & & B_p \\ | & & | \end{bmatrix} = \begin{bmatrix} | & & | \\ AB_1 & & AB_p \\ | & & | \end{bmatrix} $$ $A$, of course, could have any geometry, but we show an example here where $A$ is a rotation matrix to help visualize that the same transformation ($A$) is happening to each column of $B$

Column-Column: Right-Multiplication

When right-multiplying by $A$ by a matrix $B$, the most natural perspective is to think of each column of $B$ as taking a linear combination of the columns of $A$. We again initially show this hear for cases where $B$ is a rotation matrix. Note the qualitative differences with the left multiplication picture above.

This perspective is maybe the most natural in general. The columns of $A$ are vectors that define a span and the columns of $B$ give coefficients of particular linear combinations. We can see how this perspective expands to products of multiple matrices by repeatedly taking linear combinations.

Other perspectives

Row-Matrix: Right-Multiplication

The row-matrix perspective is the same as the matrix-column perspective but with the role of rows and columns (and the direction of mutiplication) reversed. Here we think of the matrix $B$ as applying a transformation to each of the rows of $A$ $$ AB = \begin{bmatrix} - & a_1^T & - \\ & \vdots & \\ - & a_m^T & - \end{bmatrix} \Big[ \ B \ \Big] = \begin{bmatrix} - & a_1^TB & - \\ & \vdots & \\ - & a_m^TB & - \end{bmatrix} $$ We do not draw any figures here as they would have precisely the same flavor as the matrix-column figures.

Row-Row: Right-Multiplication

Similarly, the row-row perspective is the same as the column-column perspective but with the role of rows and columns (and the direction of mutiplication) reversed. Again we do not draw any new figures to avoid rendundancy.

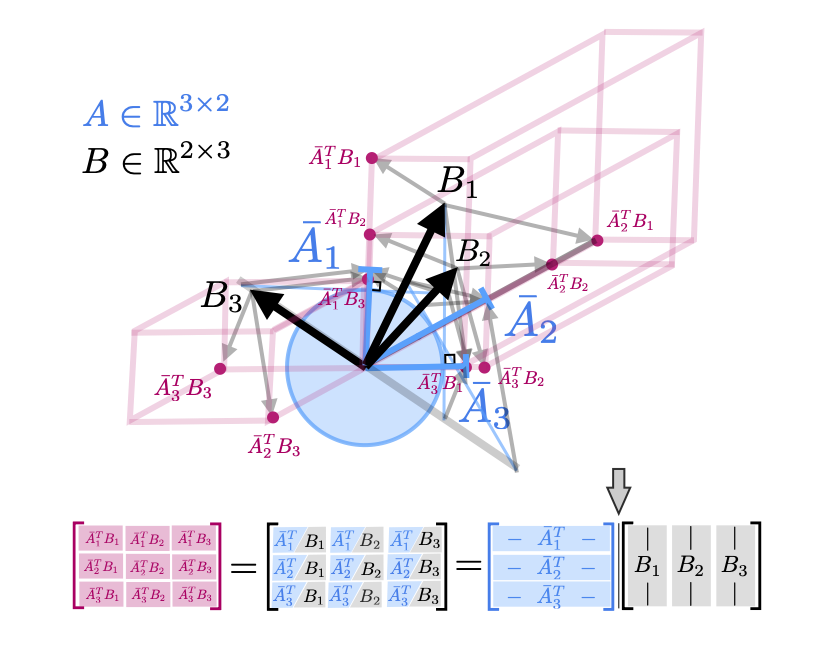
Row-Column Geometry: Pairs of Inner Products

We conclude with two perspectives that combine the row and column geometry of the matrices and are thus slightly more abstract. The first is that $AB$ computes each pairwise inner product between the rows of $A$ and the columns of $B$ $$ AB = \begin{bmatrix} - & a_1^T & - \\ & \vdots & \\ - & a_m^T & - \end{bmatrix} \begin{bmatrix} | & & | \\ B_1 & & B_p \\ | & & | \end{bmatrix} = \begin{bmatrix} a_1^TB_1 & \cdots & a_1^TB_p \\ \vdots & & \vdots \\ a_m^TB_1 & \cdots & a_m^TB_p \end{bmatrix} $$ in a loose sense this can be thought of as the projection of the columns of $B$ onto the rows of $A$ (or the rows of $A$ onto the columns of $B$). Unlike the previous perspectives which consider the product as rows or columns, this perspectives treats the product matrix as individual values.

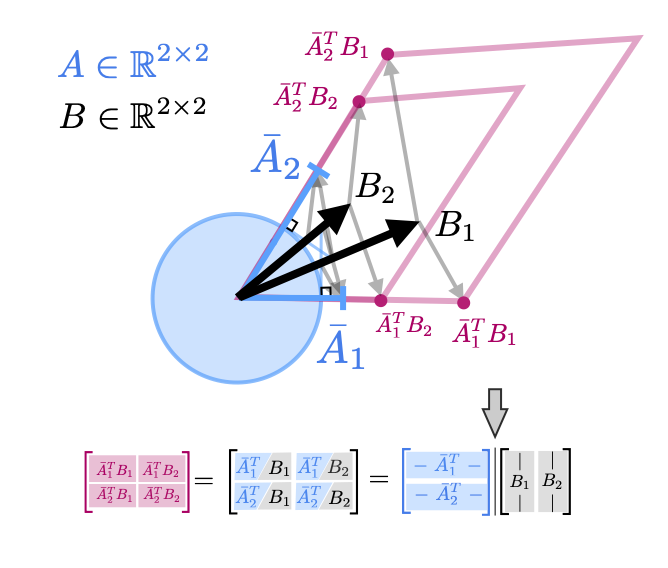
We illustrate this perspective first when both $A$ and $B$ are in $\mathbb{R}^{2 \times 2}$.

We then illustrate this perspective for $A \in \mathbb{R}^{3 \times 2}$ and $B \in \mathbb{R}^{2 \times 3}$. Note that since we are projecting the rows of $A$ onto the columns of $B$ we are considering the geometry in the space between $A$ and $B$, in this case $\mathbb{R}^2$.

Column-Row Geometry: Sum of Outer Products

The final perspective is to treat $A$ as columns and $B$ as rows. The product is then the sum of all the outer products of each column of $A$ and the corresponding row of $B$. Like the row-column geometry, this perspective does not treat the product $AB$ as rows or columns but rather as a sum of full matrices. We illustrate this geometry below. This is perhaps the most difficult visualize as visualizing outer products relies on somewhat on seeing parallel axis representation of the row vectors which is less natural.

The following interactive visualization allows us to experiment with the column and row geometry for several matrices multiplied together.