If any of the columns of a matrix \(A\) are linear combinations of other columns, then different sets of coordinates \(x\) could(will) produce the same resulting \(Ax\). For example, suppose for a \(3\times3\) matrix \(A\) the third column is a linear combination of the first two columns, ie. $$ \begin{bmatrix} | \\ A_3 \\ |\end{bmatrix} = \begin{bmatrix} | \\ A_1 \\ |\end{bmatrix} w_1 + \begin{bmatrix} | \\ A_2 \\ |\end{bmatrix} w_2 $$ Note then that we get \(Ax=\mathbf{0}\) if we choose \(x\) in the following way $$ Ax = \begin{bmatrix} | & | & | \\ A_1 & A_2 & A_3 \\ | & | & | \\ \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ -1 \end{bmatrix} = \begin{bmatrix} | \\ \mathbf{0} \\ | \end{bmatrix} $$ The vector \(x\) is said to be in the "nullspace" of \(A\) since \(Ax=\mathbf{0}\). In other words, elements in the nullspace are coordinates of 0.
We can use this idea to generate vectors in the nullspace of \(A\). (We will show later these vectors actually form a basis for nullspace of \(A\).) For illustration purposes consider \( A \in \mathbb{R}^{ 2\times 5} \) $$ A = \begin{bmatrix} | & | & | & | & | \\ A_1 & A_2 & A_3 & A_4 & A_5 \\ | & | & | & | & | \end{bmatrix} $$ where the first two columns are linearly independent. In this case, columns 3, 4, and 5 can be written as linear combinations of the first two columns. We then have the following way of constructing non-zero "coordinates of the origin" , ie. vectors in \(N_i \in \mathbb{R}^5\) such that \(AN_i = 0\). We illustrate this construction below.
We note also that we can use this construction to visualize the nullspace in the co-domain as well.
In general for an \(m \times n\) matrix \(A\), suppose that all the columns of \(A\) lie in the span of the first \(k\) columns. we can extend the above technique to construct elements in the nullspace of \(A\) as follows. Let \(B_j \in \mathbb{R}^k\) be the coordinates of column \(A_j\) with respect to the first \(k\) columns of \(A\), ie. $$ \begin{bmatrix} | \\ A_j \\ |\end{bmatrix} = \begin{bmatrix} | & & | \\ A_1 & \cdots & A_k \\ | & & | \\ \end{bmatrix} \begin{bmatrix} | \\ B_j \\ |\end{bmatrix} $$ It follows then all the columns of the a matrix \(N \in \mathbb{R}^{n \times n-k}\) given below are in the nullspace of \(A\) $$ AN = \Bigg[ \ \ A' \quad A'' \ \ \Bigg] \begin{bmatrix} B \\ -I_{k+1} \end{bmatrix} = \Bigg[ \ \ \mathbf{0} \ \ \Bigg] $$ where $$ B = \begin{bmatrix} | & & | \\ B_{k+1} & \cdots & B_n \\ | & & | \end{bmatrix} $$ and $$ A' = \begin{bmatrix} | & & | \\ A_{1} & \cdots & A_k \\ | & & | \end{bmatrix} \ \ A'' = \begin{bmatrix} | & & | \\ A_{k+1} & \cdots & A_n \\ | & & | \end{bmatrix} $$ We can actually show that the columns of \(N\) constructed this way are actually a basis for the nullspace of \(A\). If we chose other columns (rather than the first \(k\)) to span the column space of \(A\), we could do the same construction but we would have to reorder the rows of \(N\).
We say the nullspace of a matrix is "non-trivial" if it contains more than the zero-vector. (The zero-vector is obviously always in the nullspace.)
If two sets of coordinates \(x\) and \(x'\) differ by an element of the nullspace, ie. \(x-x'\) is in the nullspace then they will both map through \(A\) to the same point $$ 0 = A(x-x') \qquad \Rightarrow \qquad Ax = Ax' $$ This means equations of the form \(y=Ax\) do not have unique solutions when \(A\) has a non-trivial nullspace.
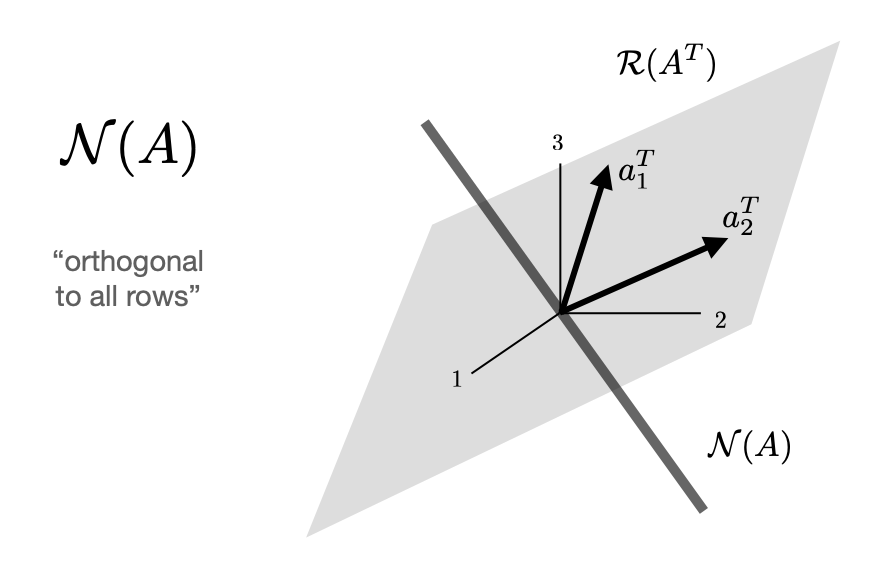
The row geometry for the nullspace of a matrix is actually somewhat simpler than the column geometry. If \(Ax = 0\) we have simply that \(x\) must be orthogonal to each of the rows of the matrix. $$ Ax = \begin{bmatrix} - & a_1^T & - \\ & \vdots & \\ - & a_m^T & - \end{bmatrix} \begin{bmatrix} | \\ x \\ | \end{bmatrix} = \begin{bmatrix} a_1^Tx \\ \vdots \\ a_m^Tx \end{bmatrix} = \begin{bmatrix} 0 \\ \vdots \\ 0 \end{bmatrix} $$ If we draw the rows of \(A\), the nullspace is simply the subspace orthogonal to each row. We illustrate this below in the \(\mathbb{R}^{1 \times 3}\) and \(\mathbb{R}^{ 2 \times 3}\) matrix cases.