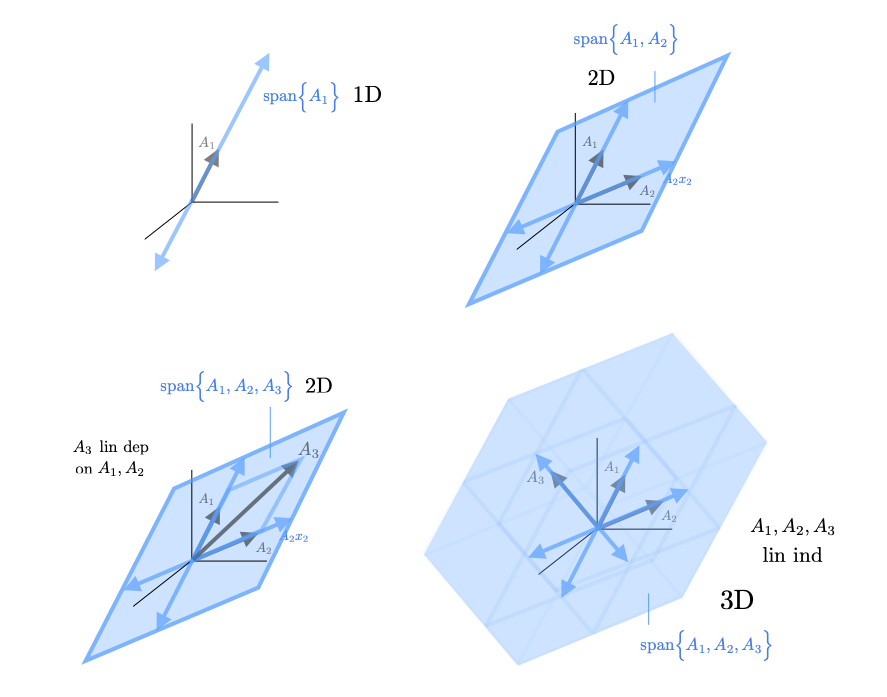
The "range" of a matrix \(A\) is the span of the columns, ie. the set of vectors \(y\) in the co-domain for which you could find an \(x\) such that \(y=Ax\). If the range of \(A\) is all of the co-domain, we say that the matrix \(A\) is onto. As a rule of thumb, fat matrices are onto (assuming there are enough linearly independent columns). If a matrix is tall (or there are not enough linearly independent columns), then there is a subspace of the co-domain that is not reachable through \(A\).
An equation of the form \(y=Ax\) for a tall \(A\) will usually not have a solution because it is not guaranteed that every \(y\) is in the range of \(A\) (in other words, \(y=Ax\) is actually false for all \(x\)'s.) At best, we can solve the equation \(\text{proj}_Ay = Ax\) where \(\text{proj}_Ay\) is the closest vector to \(y\) within the range of \(A\). This is the well-studied "least-squares solution" in which we choose \(x\) to minimize the norm-squared of \(y-Ax\) $$ \min_x \quad \big|\big|y-Ax \big|\big|^2_2 = (y-Ax)^T(y-Ax) $$ with the the optimal \(x\) given by $$ x = (A^TA)^{-1}A^Ty $$ \(Ax\) is then given by $$ Ax = A(A^TA)^{-1}A^Ty $$ (which is the projection of \(y\) onto the range of A).