General Case
Changing the basis of the domain and co-domain of a matrix \(A\) naturally affects the representation of \(A\). Suppose we have the matrix equation \(y=Ax\) for \( A \in \mathbb{R}^{m \times n}\) and we apply the two coordinate transformations \(x = Vx'\) and \(y = Wy'\) to the domain and co-domain respectively. A new matrix \(A' \in \mathbb{R}^{m \times n}\) that performs the same transformation but between the \(x'\) and \(y'\) coordinates can be derived simply $$ y = Ax \qquad \Rightarrow \qquad Wy' = AVx' \qquad \Rightarrow \qquad y' = W^{-1}AV x' $$ we then have $$ A' = W^{-1}AV $$ Note that this construction is general and works for and size \(A\) as long as \(V\) and \(W\) are square and invertible of the appropriate dimensions. We illustrate the relationship between the representations of the domain and co-domain and the maps \(A\) and \(A'\) in the following diagram.
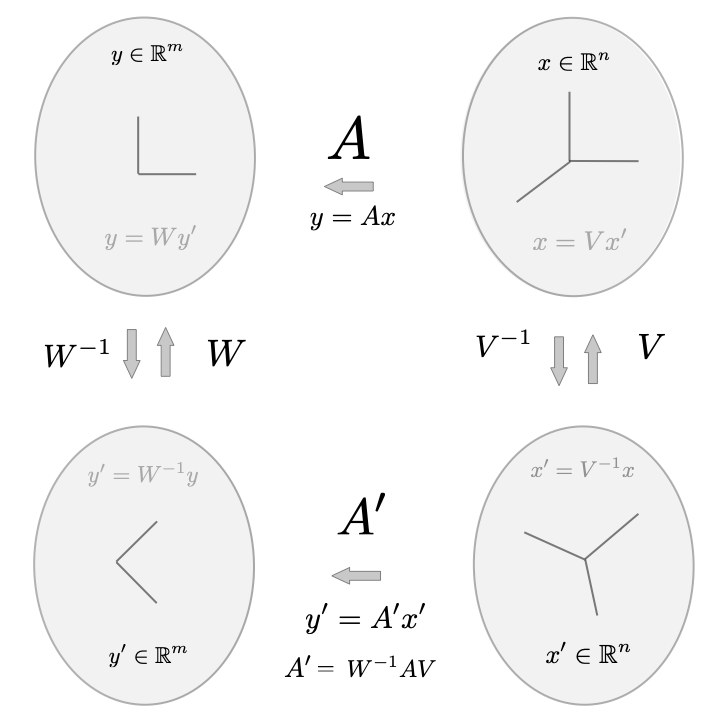
We note that it is instructive to think explicitly about the action of \(A'\) in terms of it's components. The action of \(A'\) on \(x'\) can be thought of as first transforming \(x'\) back into the \(x\) coordinates, \(Vx'\); then applying the original map \(A\) to the result \(AVx'\); and then finally transforming into the \(y'\) coordinates, \(W^{-1}AVx'\).
Very often the matrix \(A\) is square and we apply the same coordinate transformation to the domain and co-domain. In this case (for coordinate transforms \(x = Vx'\) and \(y = Vy'\)), the above construction becomes $$ A' = V^{-1}AV $$ In this case, we say that \(A\) and \(A'\) are similar to each other and the above equation is called a similarity transform. We will see later that similarities tranforms preserve eigenvalues and thus the fundamental internal structure of a linear map. We reproduce the figure above since it is commonly seen in linear algebra analysis.

We end with several interactive visualizations that show the relationship between \(A\) and \(A'\) in a much more explicit sense given the row and column geometry of the matrices. Again, to simplify the intution we first use orthonormal transformations (rotations) for \(V\) and \(W\) (tho of course this is not required). We show this visualization for the non-square and square case.
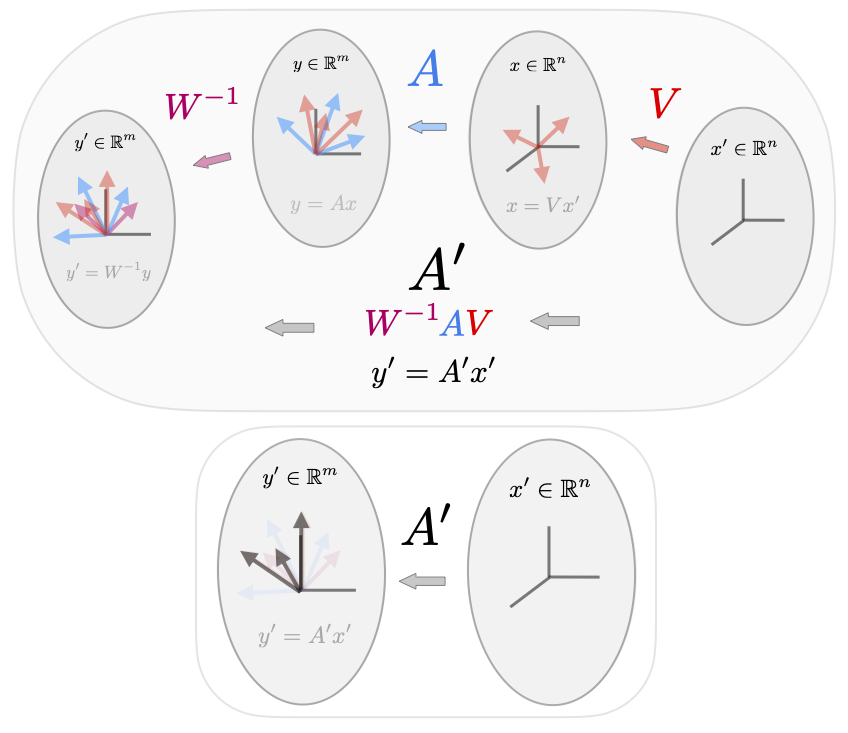
Finally, we show the geometry of the general case when \(V\) and \(W\) are not rotations.