The following is a supplemental exposition of some of the results in the following manuscripts.

• Calderone, D.J. , and Ratliff, L.J., Multi-Dimensional Continuous-Type Population Potential Games: Primal-Dual Formulations 2024 - SUBMITTED
• Calderone, D.J. , Khanna, A., Dubey A., and Ratliff, L.J., A Hybrid Routing Game/Vehicle Routing Approach to Multi-Modal Transportation Choice in Chattanooga Tennesse 2024 - IN PREPARATION
• Calderone, D. and Ratliff, L.J., December. Multi-Dimensional Continuous Type Population Potential Games. In 2019 IEEE 58th Conference on Decision and Control (CDC) (pp. 5138-5143). IEEE. pdf talk

Overview

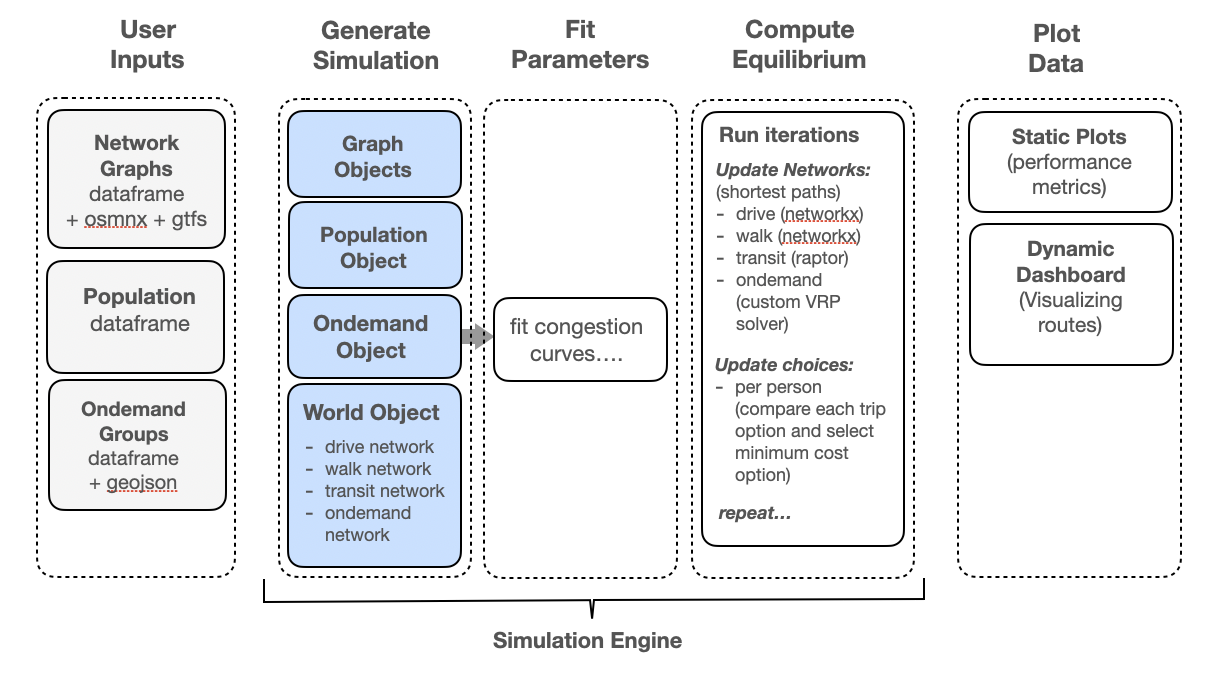
In this work, we develop a simulation engine for studying multi-modal traffic problems. We use a hybrid framework that combines traditional static routing game models for driving and walking modes with more complicated temporal models such as an implementation of RAPTOR for fixed-line transit and VRP solvers (vehicle routing problem) for ondemand transit services. The goal of this hybrid framework is to be flexible and lightweight. The focus of our model is understanding tradeoffs between ondemand transit services and fixed-line transit in Chattanooga, TN (CARTA).

Python Dependencies

The simulation framework was developed in Python. Street network information is imported and stored using the Open Street Map package OSMnx which is built on the general graph manipulation package NetworkX. Fixed line transit information is imported using standard GTFS format (General Transit Feed Specification) using the package gtfs-functions. Routing game solvers, RAPTOR solvers, and vehicle routing problem (VRP) solvers are implemented on top of these packages.

Sample Dashboard

Below is a sample an interactive dashboard from the output of the model showing origin/destination information for agents in the population and trip segments for different travel models including driving (red), walking (yellow), ondemand transit (blue), and fixed line transit (orange).

Optimal Routes: Modeling Paradigms

The simulation framework currently supports four modes of transportation: driving, walking, ondemand transit , fixed line transit . Each mode uses a slightly different modeling paradigm depending on which factors (such as congestion, timing of trips, line transfers, etc) are important to be realistic. Here we give details of the modeling choices and solvers for each mode.

The simulation framework was developed in Python. Street network information is imported and stored using the Open Street Map package OSMnx which is built on the general graph manipulation package NetworkX. Fixed line transit information is imported using standard GTFS format (General Transit Feed Specification) using the package gtfs-functions. Implementations routing game solvers, RAPTOR solvers, and vehicle routing problem (VRP) solvers are implemented on top of these packages.

• Driving & Walking ,

  Packages: OSMnx, NetworkX

  Modeling Paradigm: Routing Games

  The driving and walking modes are handled using a traditional static nonatomic routing game framework for congestion. In this framework, the network is modeled by a graph \(\mathcal{G} = (\mathcal{V},\mathcal{E})\) with nodes \(\mathcal{V}\) modeling intersections and edges \(\mathcal{E}\) modeling streets/footpaths. Each street in the network \(e \in \mathcal{E}\) is associated with a flow variable \(x_e \in \mathbb{R}_+\) that denotes how much population flow per unit time (cars/min, etc) and a latency function \(\ell_e(x_e)\) which gives the travel time for taking a particular edge depending on usage. Congestion effects are modeled by the fact that the congestion function is usually taken to be positive, monotonically increasing function of flow. Different origin-destination pairs each create separate edge flows that are added together to compute total flow on each edge. Equilibrium flows are determineda according to the well-known Wardrop equilibrium principle. More details can be found in the literature. The following reference provides a (comprehensive) review and exposition.

  • Patriksson, M., 2015. The traffic assignment problem: models and methods. Courier Dover Publications.
  Given the traffic equilibrium, shortest paths for individuals are computed using implementations of Dijkstra/A\(^*\) given in NetworkX.

• Fixed Line Transit,

  Packages: gtfs-functions. OSMnx, NetworkX

  Modeling Paradigm: RAPTOR

  Fixed line transit information is imported in GTFS format. Given trip start times, optimal routes are computed using the "novel RoundbAsed Public Transit Optimized Router" algorithm (RAPTOR) developed by Microsoft Research as detailed in this paper. Our implementation is built off the implementation developed here .

• Ondemand/Micro-Transit,

  Packages: OSMnx, NetworkX

  Modeling Paradigm: VRP Solver

  Planning for ondemand/micro-transit is done using a VRP solver package developed by Michael Wilbur, et al. at Vanderbilt University. Details of the implementation are given in this paper.

  Michael Wilbur, Salah Kadir, Youngseo Kim, Geoffrey Pettet, Ayan Mukhopadhyay, Philip Pugliese, Samitha Samaranayake, Aron Laszka, and Abhishek Dubey. "An online approach to solve the dynamic vehicle routing problem with stochastic trip requests for paratransit services." In ACM/IEEE 13th International Conference on Cyber-Physical Systems (ICCPS). IEEE, April 2022

Individual Choice: Multi-factor Discrete Choice Model

Given the state of the network at equilibrium (as determined by the equilibrium models detailed in the previous section), each individual considers several possible trips from their origin to destination including different combinations of driving, walking, taking ondemand/microtransit from origin to destination and taking fixed-line transit with a walking and/or ondemand segment at either end. Each possible trip is given a cost based on a weighted sum of various factors for the trip. Factors include travel time, monetary cost, and number of (mode or fixed line) switches required. Other arbitrary convenience factors can be added as well. The cost per trip is determined by the following weighted sum for trip segments (seg) for each individual agent (agnt). $$ \begin{aligned} \text{COST}_{\text{trip}}^{\text{agnt}} & = \sum_{\text{seg}} \bigg[ w^{\text{agnt}}_{\text{t}}(\text{TIME})_{\text{seg}} + w^{\text{agnt}}_{\text{m}}(\text{MONEY})_{\text{seg}} + \\ & \qquad \qquad w^{\text{agnt}}_{\text{s}}(\text{SWITCH})_{\text{seg}} + w^{\text{agnt}}_{\text{c}}(\text{CONVEN})_{\text{seg}} \bigg] \end{aligned} $$ for individual weights \(w^{\text{agnt}}_{\text{t}}\,w^{\text{agnt}}_\text{{m}}\,w^{\text{agnt}}_\text{{s}}, w^{\text{agnt}}_\text{{c}}\). Each individual then chooses the trip with the lowest overall cost according to their individual weighted sum.

Equilibrium Computation Algorithm

The simulation runs through an iterative process till convergence. At each iteration, the projected cost per trip segment is computed for each travel mode and then each individual updates their trip choice based on the weighted costs per trip. The update algorithm for the equilibrium is an extension of a dual algorithm for the traffic assignment problem. More details will be presented in this manuscript.

• Calderone, D.J. , Khanna, A., Dubey A., and Ratliff, L.J., A Hybrid Routing Game/Vehicle Routing Approach to Multi-Modal Transportation Choice in Chattanooga Tennesse 2024 - IN PREPARATION

System Architecture

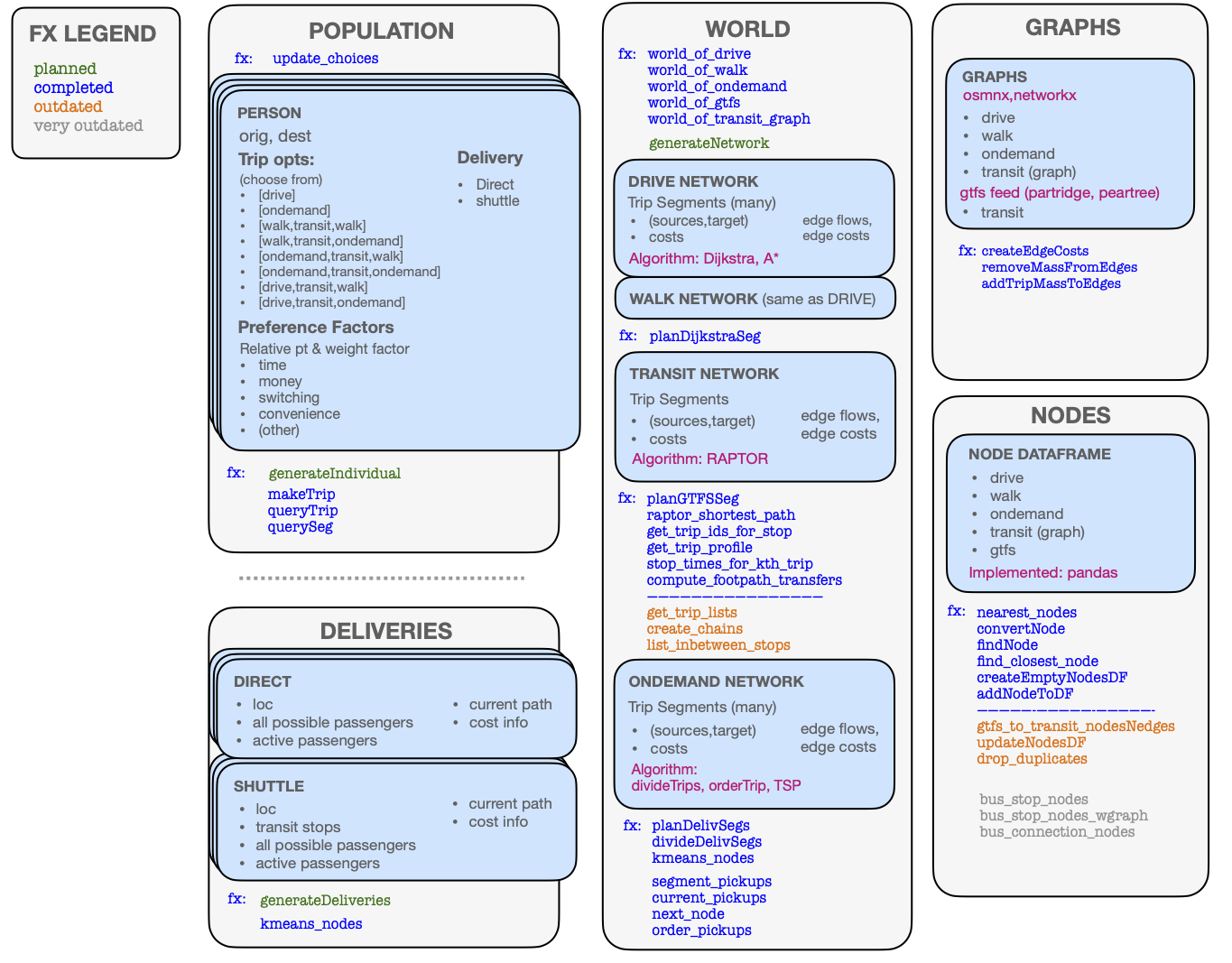
The following graphic provides a brief overview of the system architecture for the simulator. More details are presented in the monograph above.