Summary:

Leveraging tools from the study of linear fractional transformations and algebraic Riccati equations, a local characterization of consistent conjectural variations equilibrium is given for two player games on continuous action spaces with costs approximated by quadratic functions. Further, a discrete time dynamical system in the space of conjectures is derived and its stability properties are characterized.

Papers:

Consistent Conjectural Variations Equilibrium: Characterization & Stability for a Class of Continuous Games. Dan Calderone, Ben Chasnov, Sam Burden, Lillian Ratliff. LCSS 2023 paper (arxiv)

Consistent Conjectural Variations Equilibrium: Dynamic Decompositions and Asymptotic Behavior. Dan Calderone, Ben Chasnov, Sam Burden, Lillian Ratliff. (IN PREPARATION) LCSS 2025

Problem Setup

As machine learning and complex prediction techniques become more ubiquitous, game theory must adapt to include models that accurately model how agents predict their opponents behavior. Nash equilibria in their traditional form do not capture this prediction behavior. Stackleberg equilibria, where a leader player predicts a follower player's optimization problem and uses this to their advantage. Consistent conjectural variations equilibria (CCVE) extend Stackleberge equilibria to the case where two players both attempt to predict their opponent's actions and optimize accordingly. The existence of computation of CCVE for two player games center around solving coupled Riccati equations as presented in this paper.

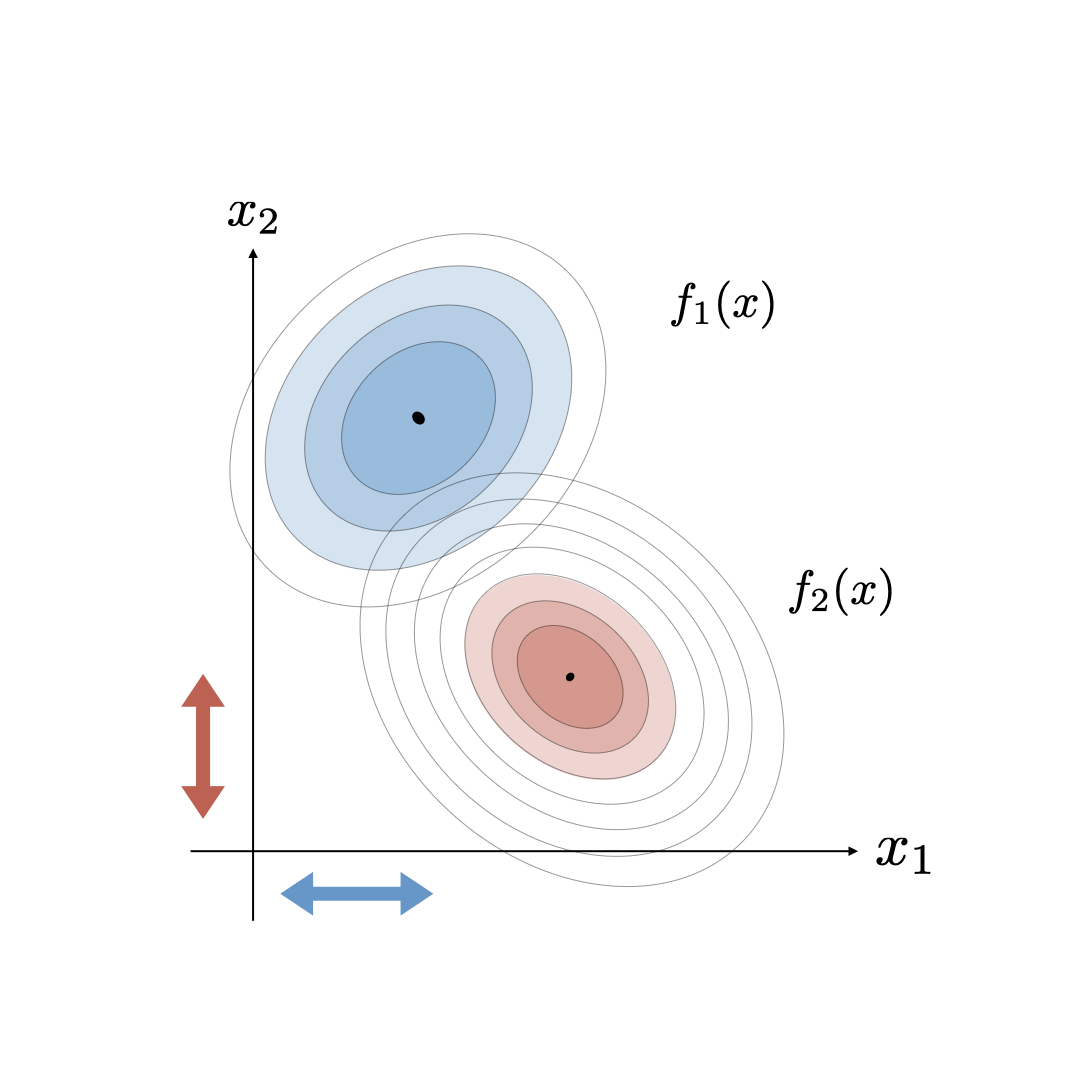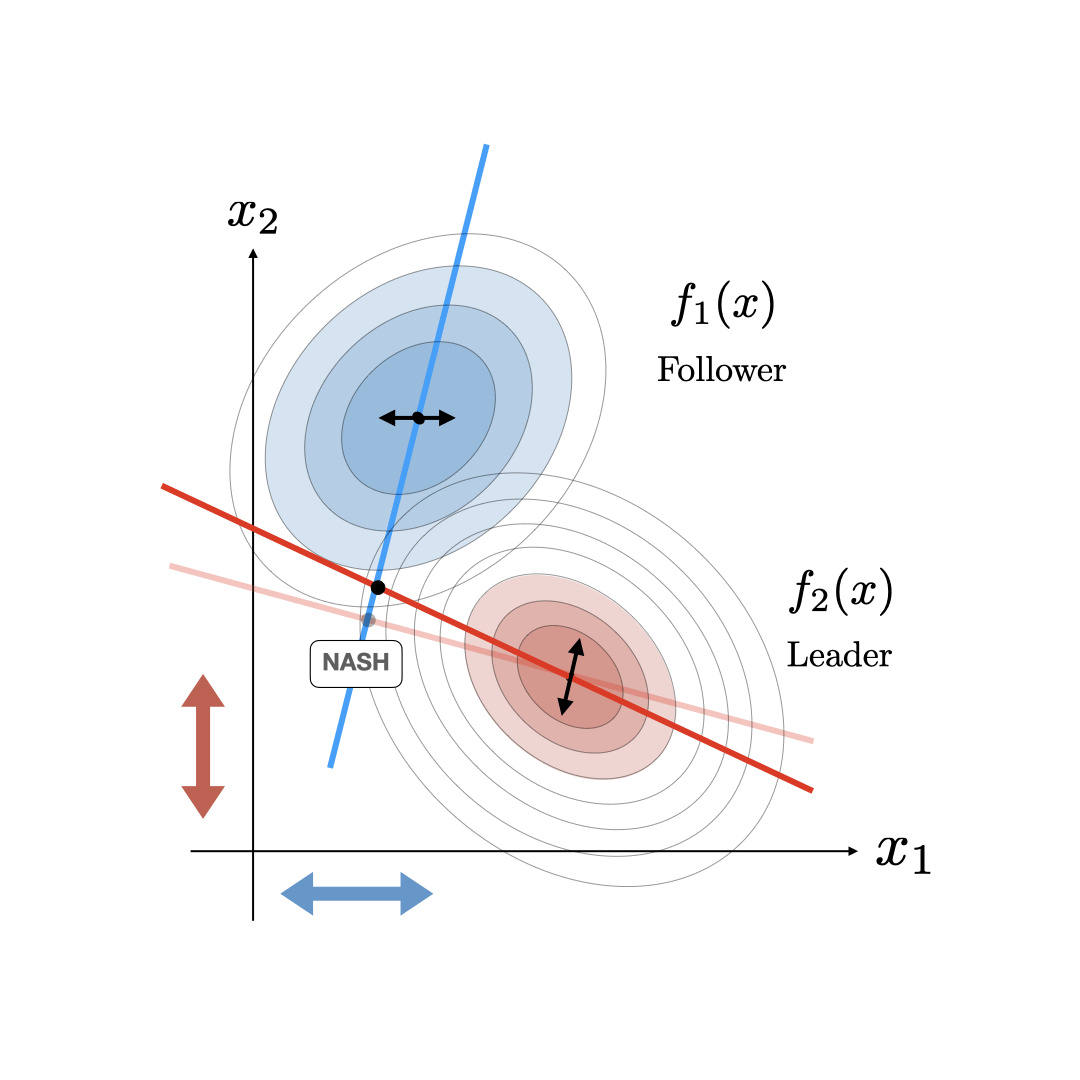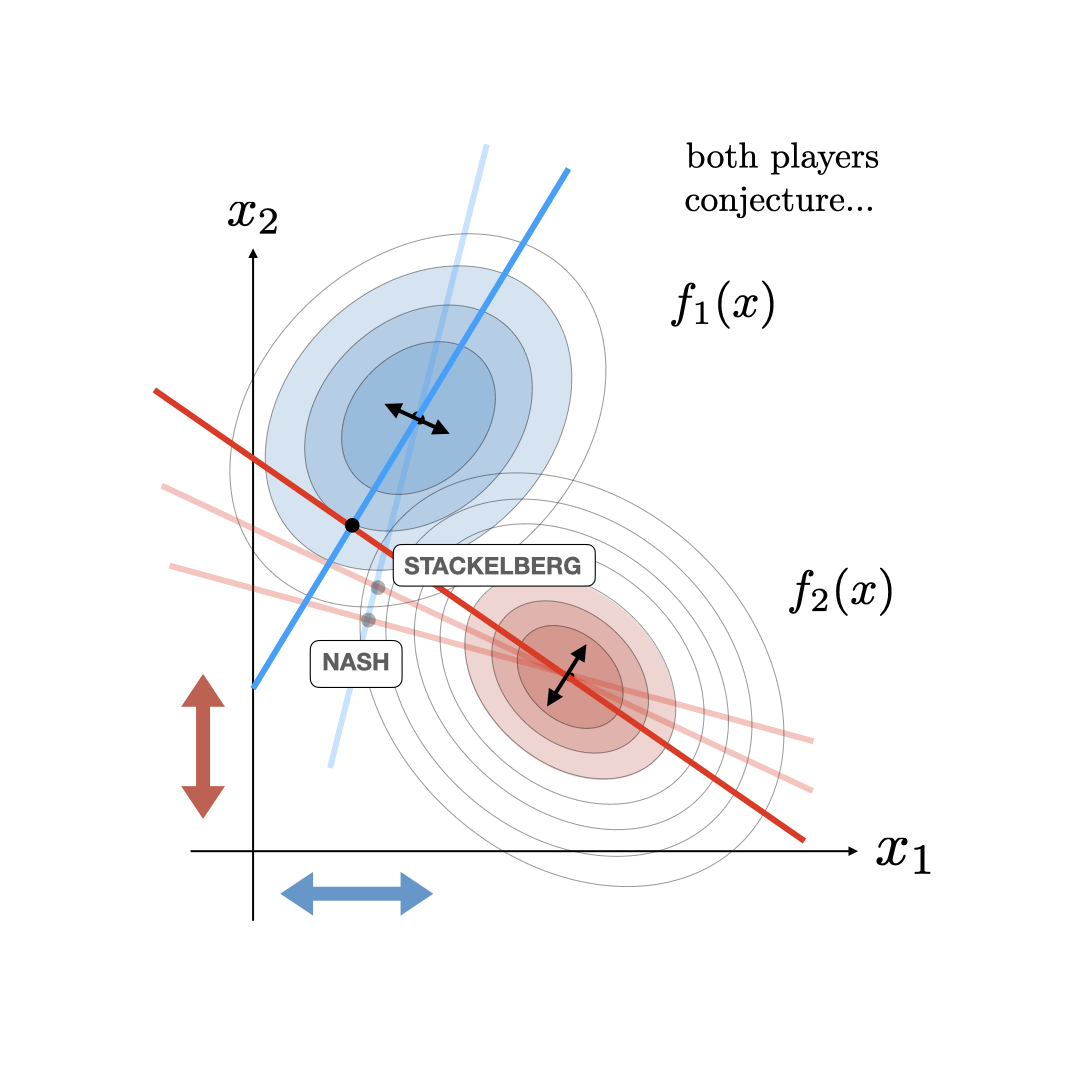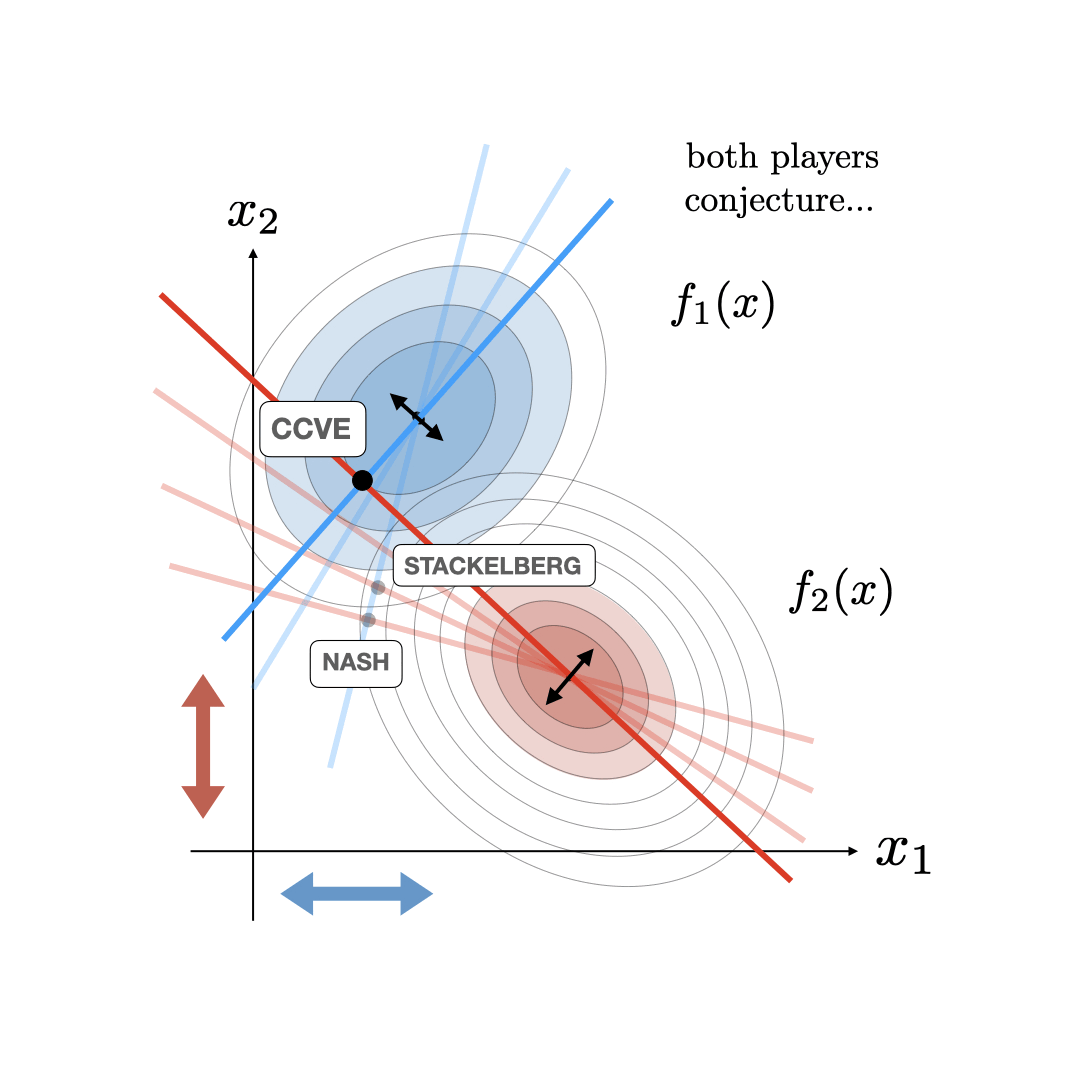
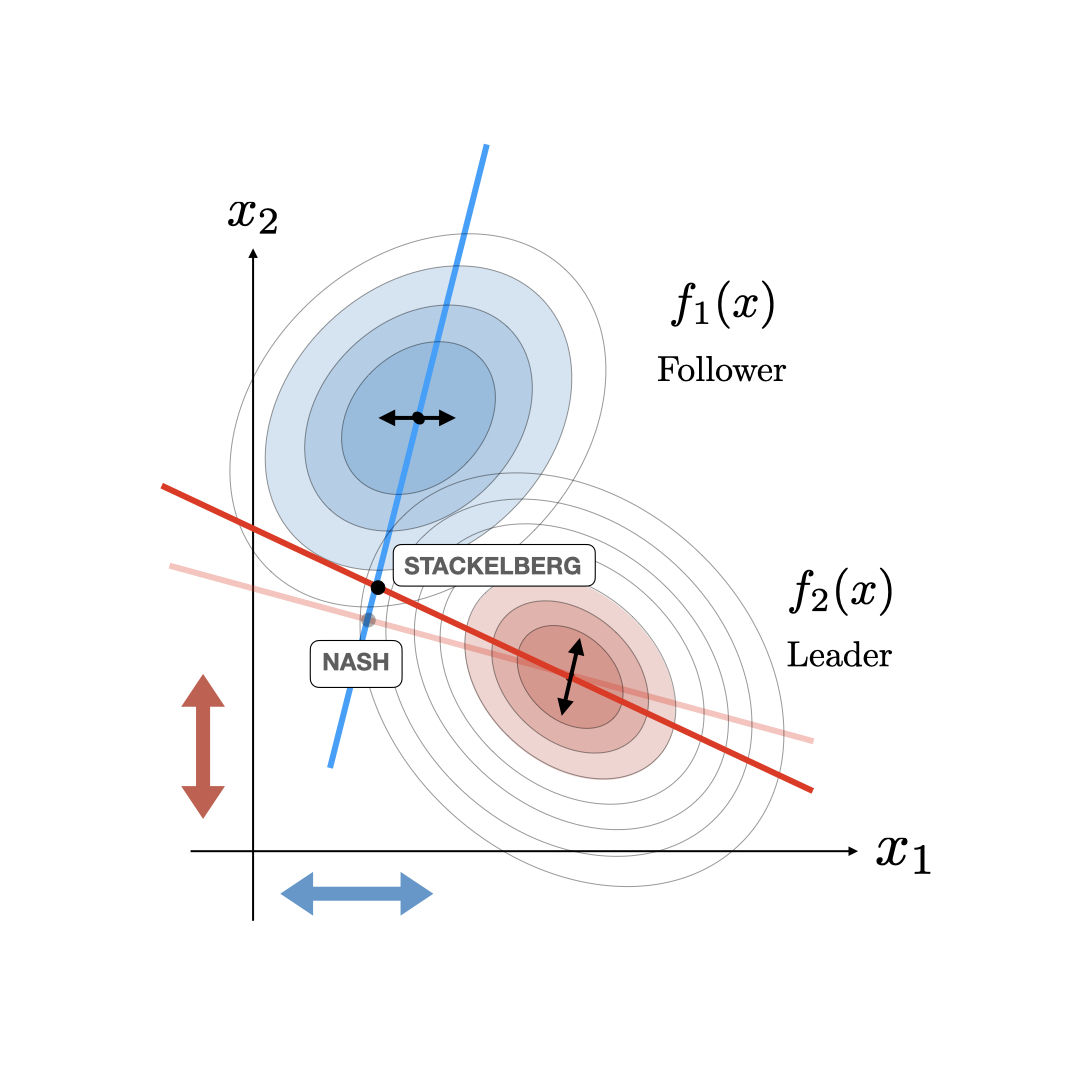
Basic Geometry: Nash and Stackelberg

In the 2D joint action case, \(u =(u_1,u_2) \in \mathbb{R}^2\), we can visualize fairly cleanly what a consistent conjectural variations equilibria looks like. Specifically, the traditional Nash equilibria is visualized by defining the optimality curves \(\partial J_1/\partial u_1=0\) and \(\partial J_2/\partial u_2=0\) and computing their intersection as visualized in the figure below. In this Stackelberg case, one of the players, the leader (in this case player 2), knows the other player (player 1's) optimality curve and can use this information to their advantage. The Stackelberg equilibria can then be visualized as the optimal point for the leader given that the joint action is constrained to the follower's optimality curve. This generates a new optimality curve for the leader (illustrated in the figure below) that intersects with player 1's optimality curve at the Stackelberg equilibrium.

Basic Geometry: CCVE

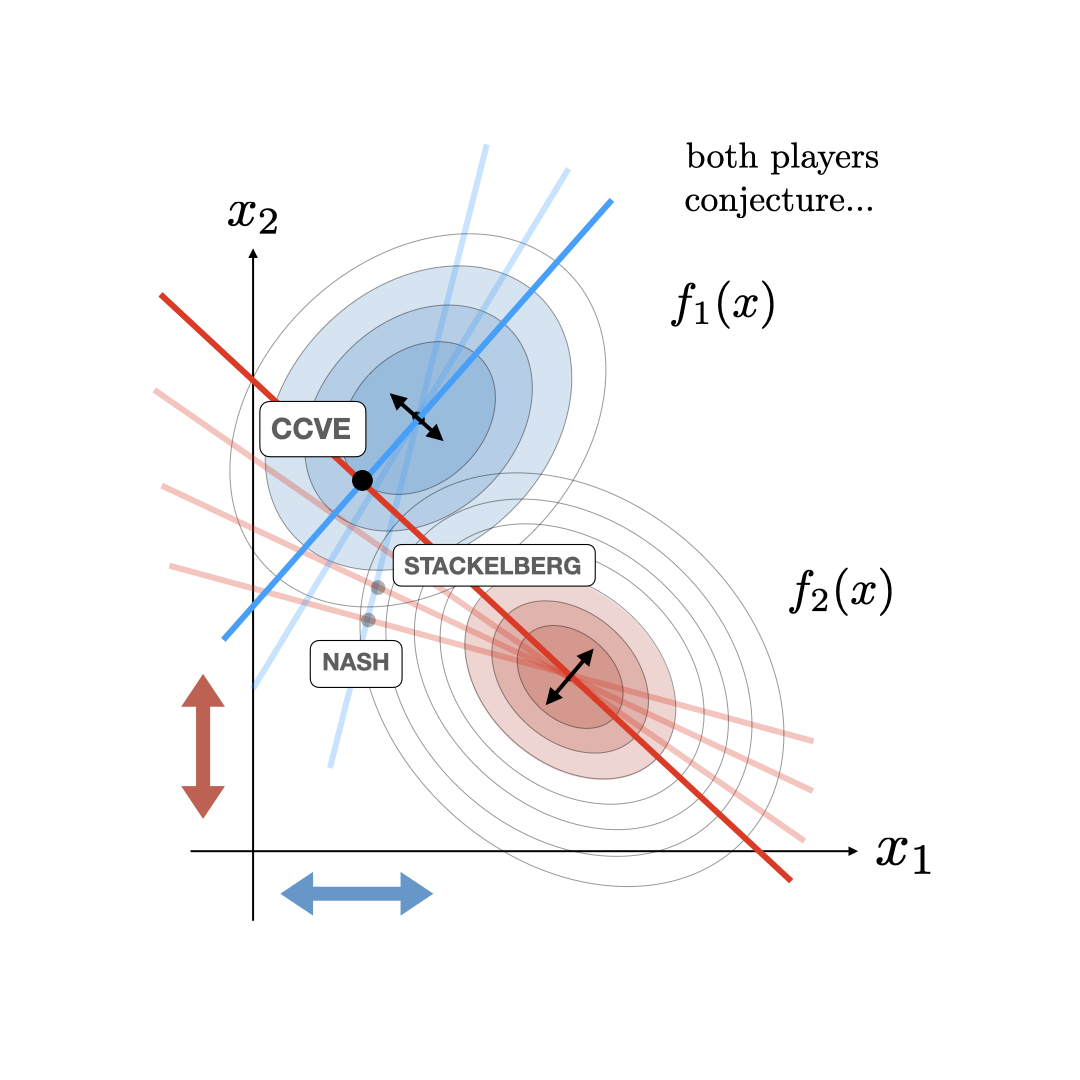
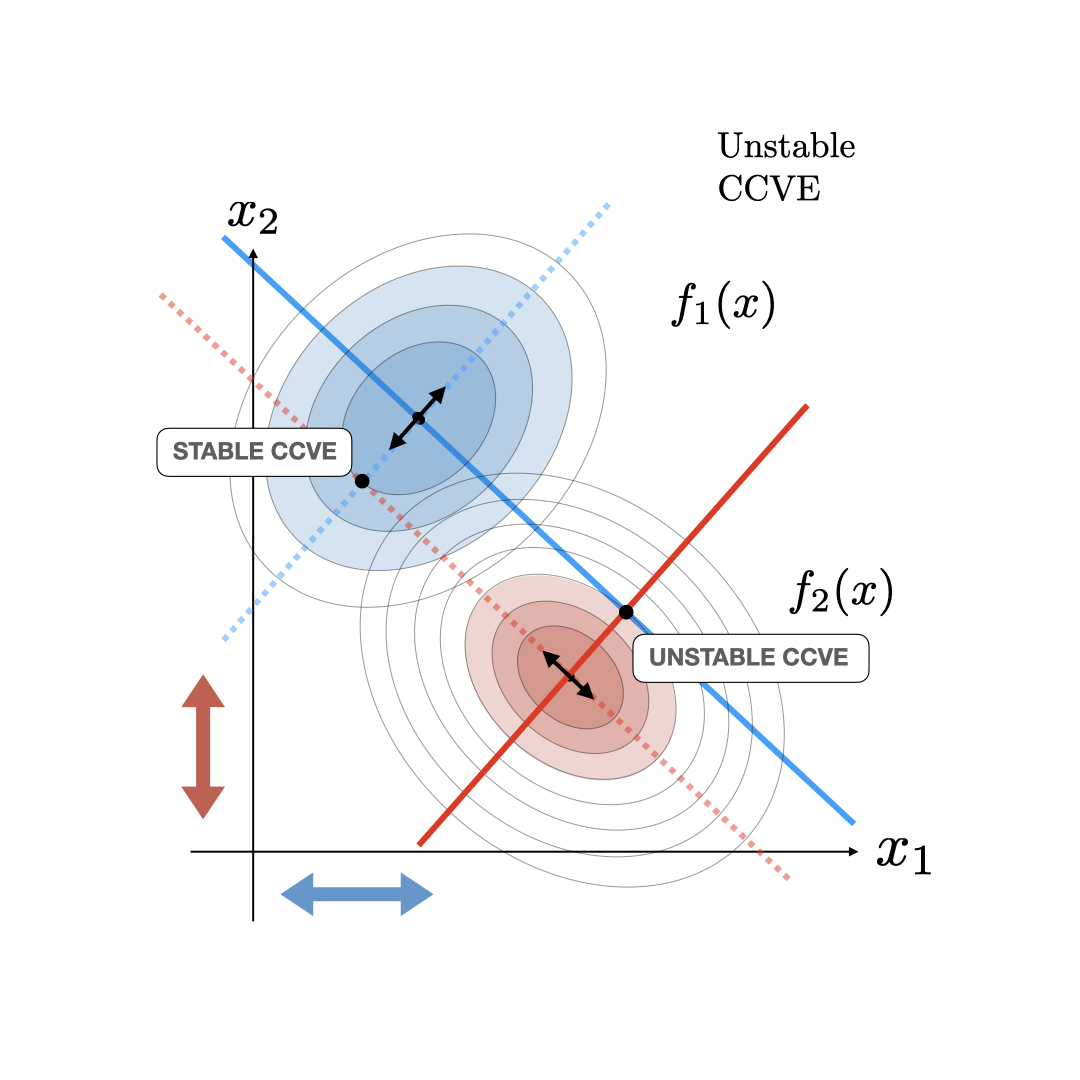
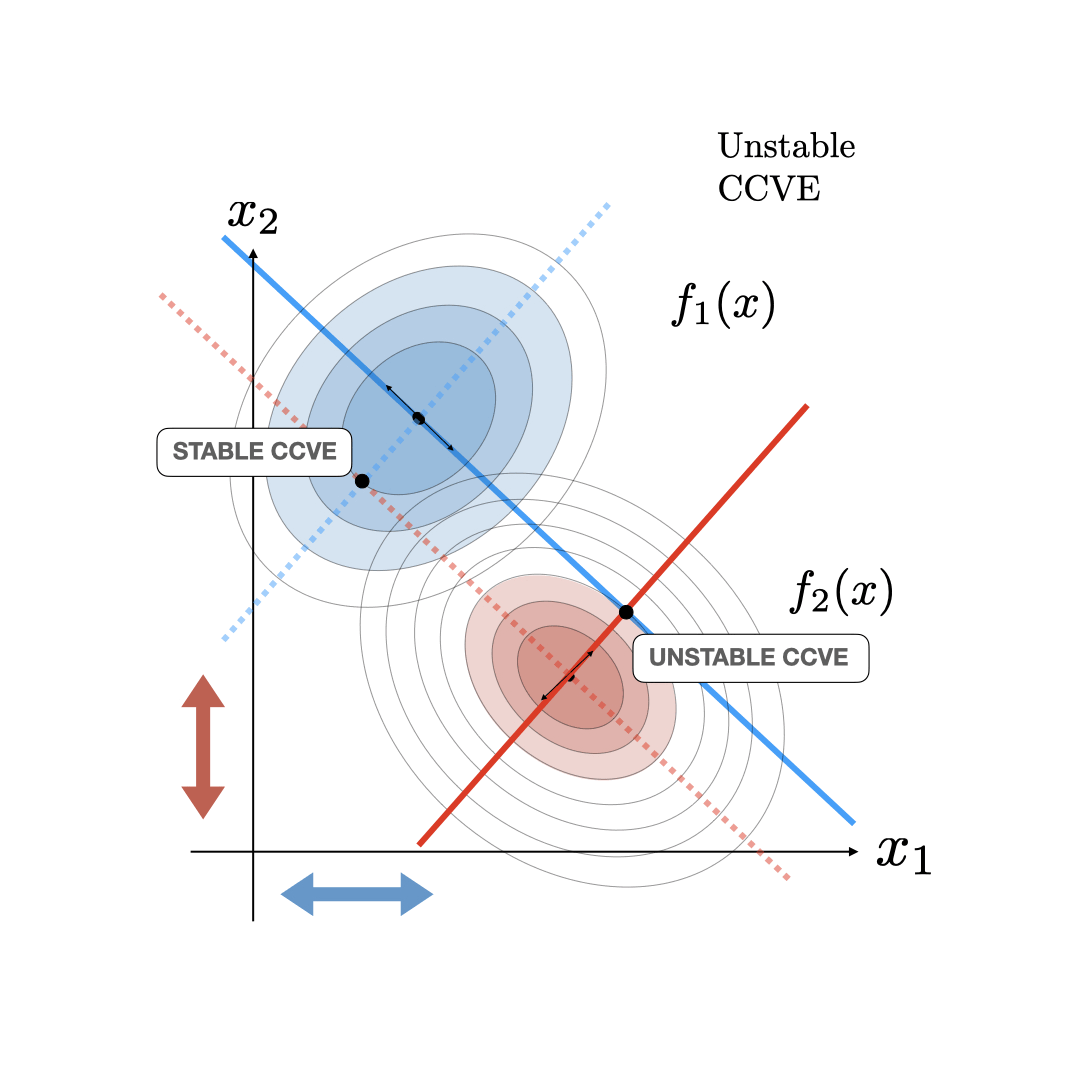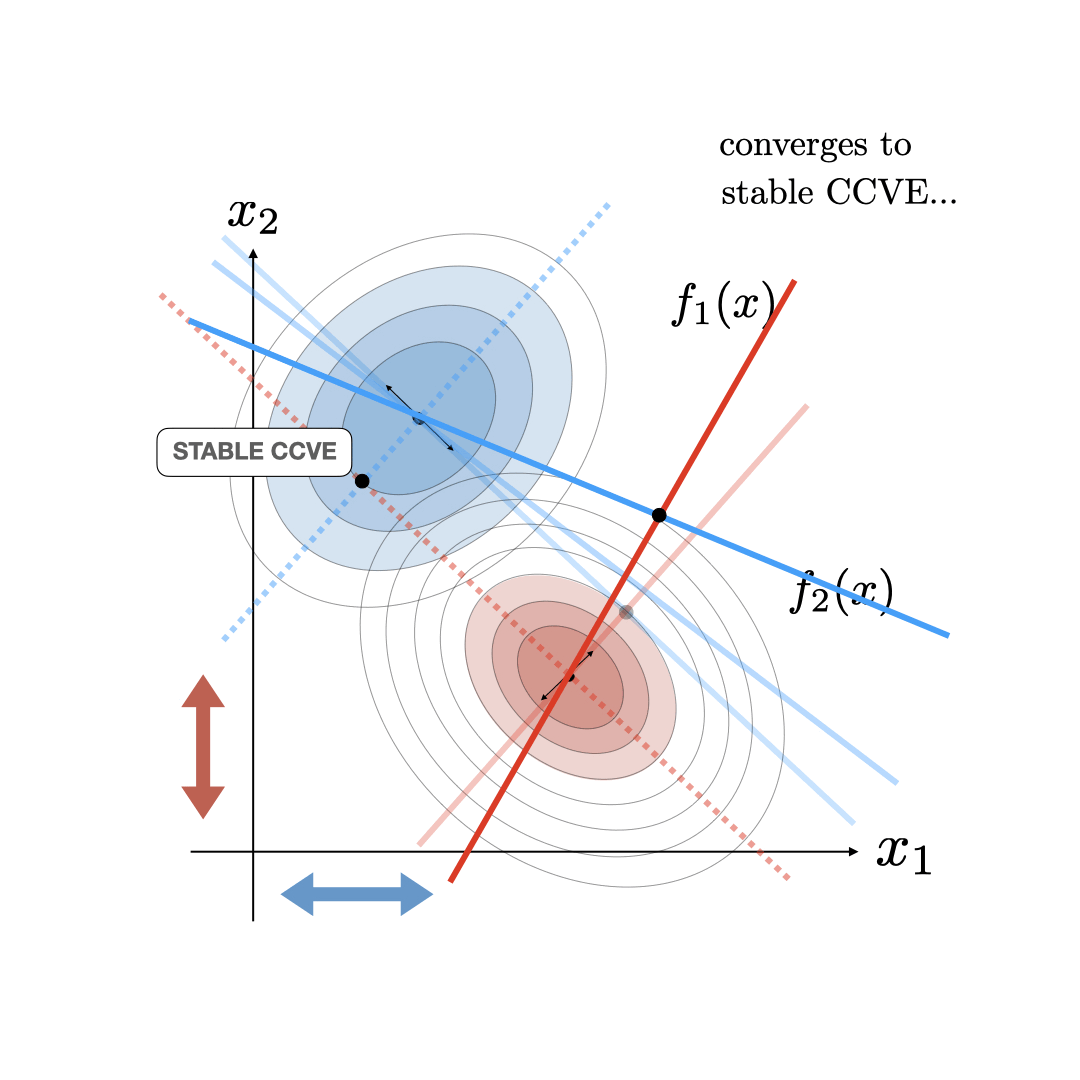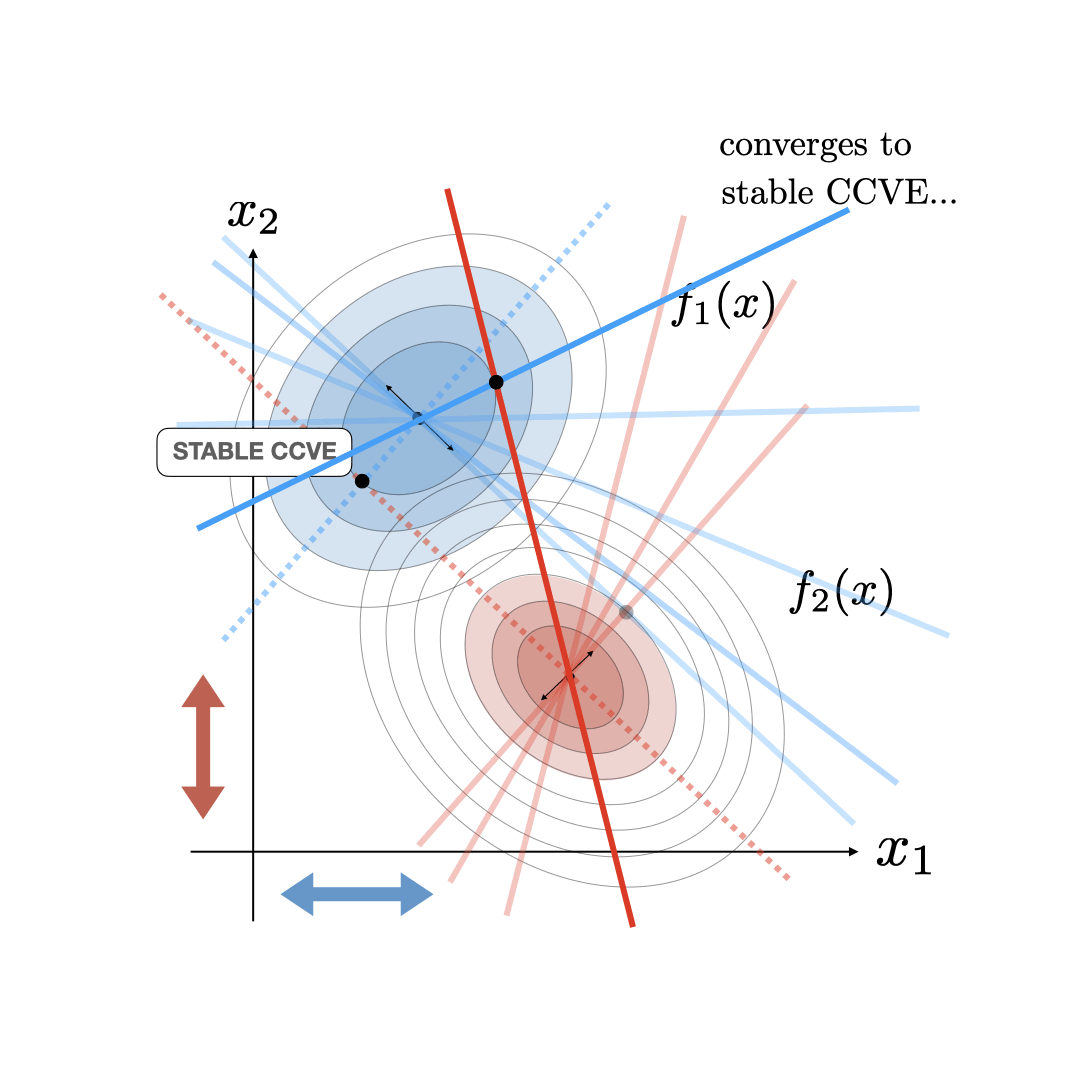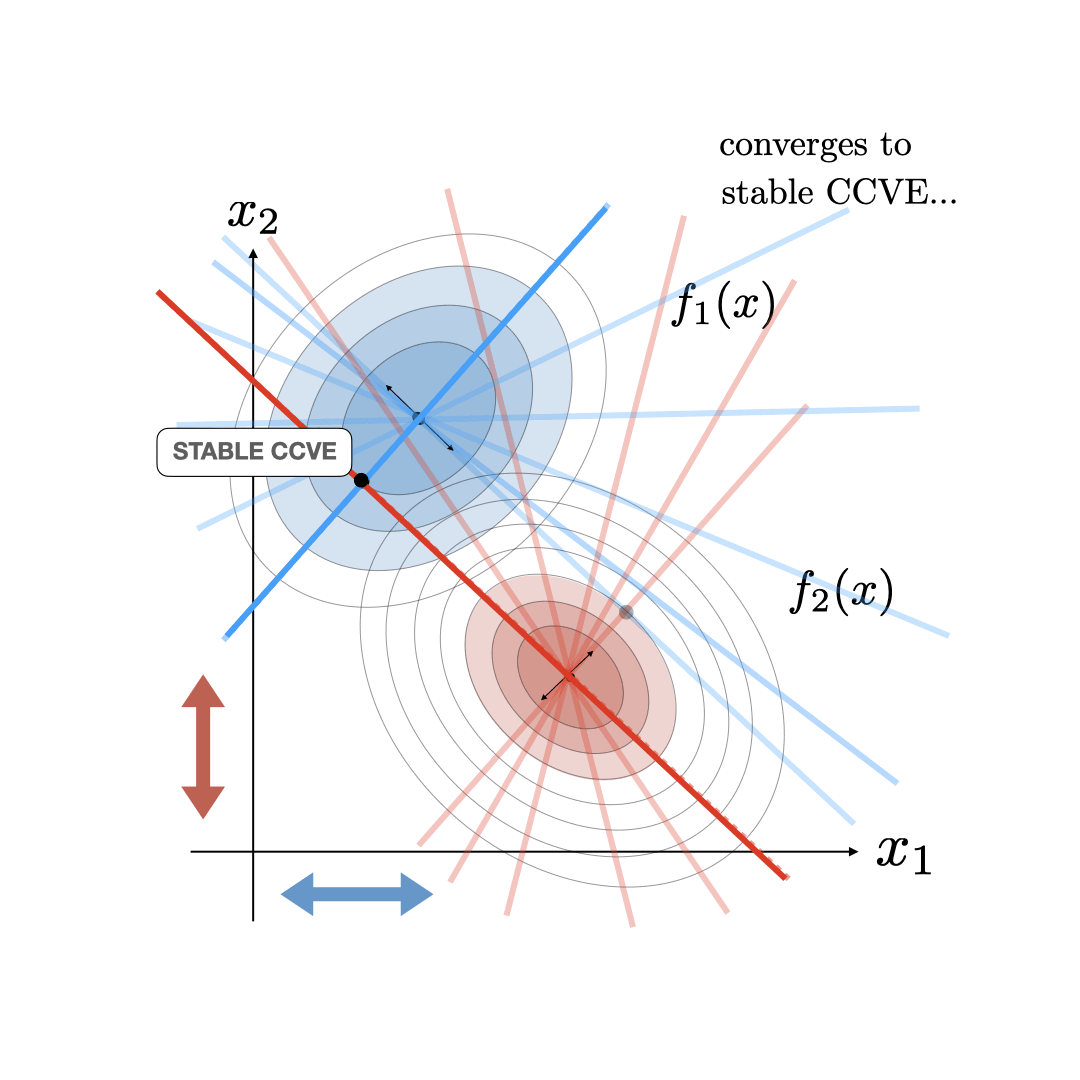
In the CCVE case, the follower player also starts acting as a leader conjecturing about the new optimality curve of the leader. This starts an iterative process where agents keep updating their estimate of their opponent's optimality curve to be consistent with their current conjecture. This process terminates at a fixed point called the consistent conjectural variations equilibrum (CCVE) where both players are finally conjecturing optimality curves for their opponents that are consistent with what they are actually doing. This CCVE equilibrium and the iterative update is illustrated below.