We consider two player quadratic games in a cooperative framework based in social value orientation, mo- tivated by the need to account for complex interactions be- tween humans and autonomous agents in dynamical systems. Social value orientation posits that each player incorporates the other player’s cost into their own objective function, based on an individually pre-determined degree of cooperation that determines the weight that a player puts on their own cost relative to the other player’s cost. We characterize the Nash equilibria under social value orientation by creating expansions that elucidate the relative difference between the Nash SVO equilibria and more typical equilibria, such as the competitive Nash equilibria, individually optimal solutions, and the altruistic solutions. Using these expansions, we show that both bounded and unbounded equilibria exist. We characterize conditions under which unbounded equilibria will occur, as well as asymptotes that the unbounded solutions follow. We apply these techniques to understand behavior in collision avoidance probems with application to driving interactions at intersections.

The Impact of Social Value Orientation on Nash Equilibria of Two Player Quadratic Games Dan Calderone, Meeko Oishi, LCSS 2025 (SUBMITTED) (arxiv)

Failure Modes from Social Value Orientation in Two-Player Open-Loop Linear-Quadratic Games Dan Calderone, Meeko Oishi. LCSS 2025 (IN PREPARATION)

We give illustrations of the four expansions given in this paper. (arxiv)

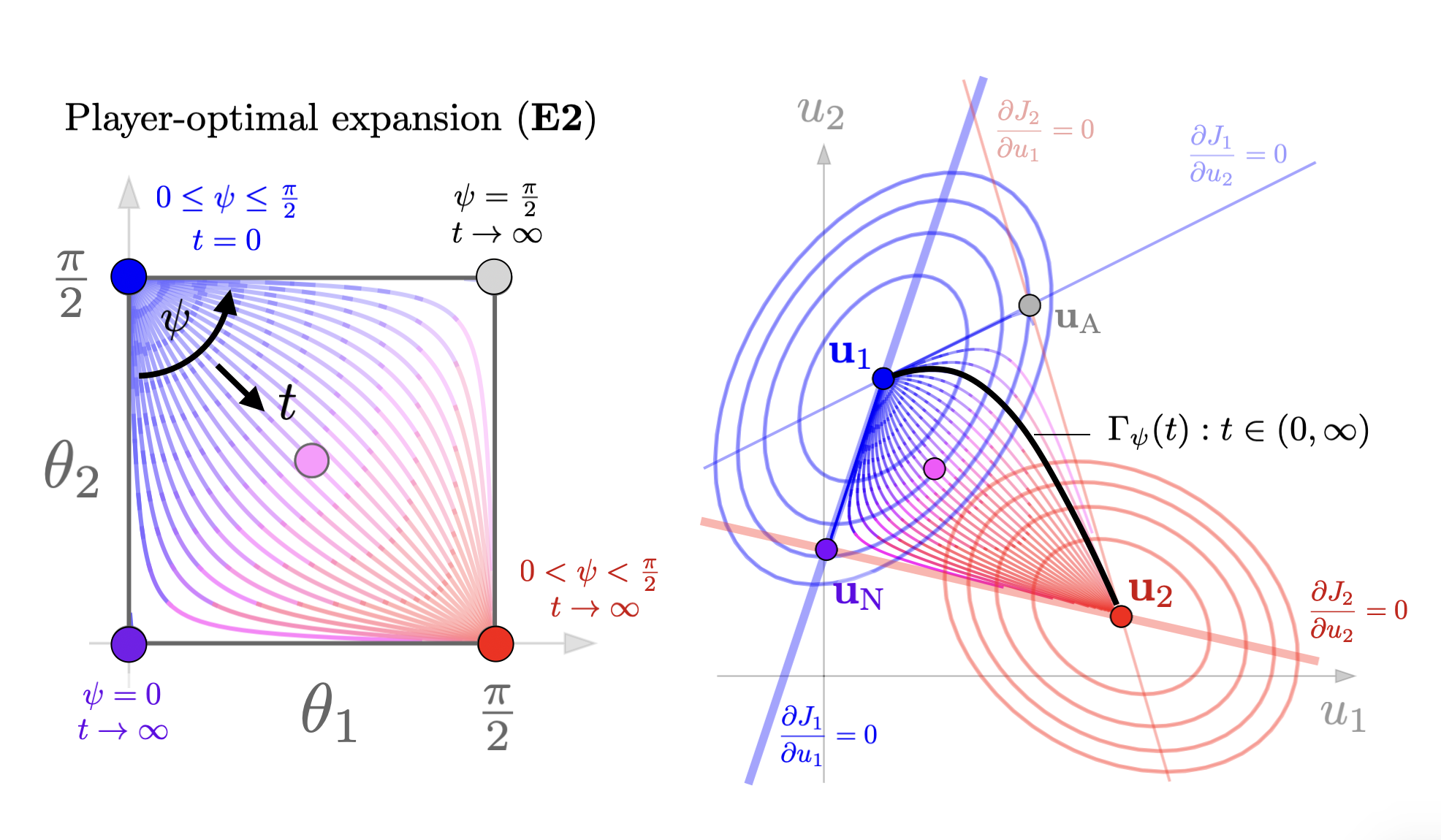
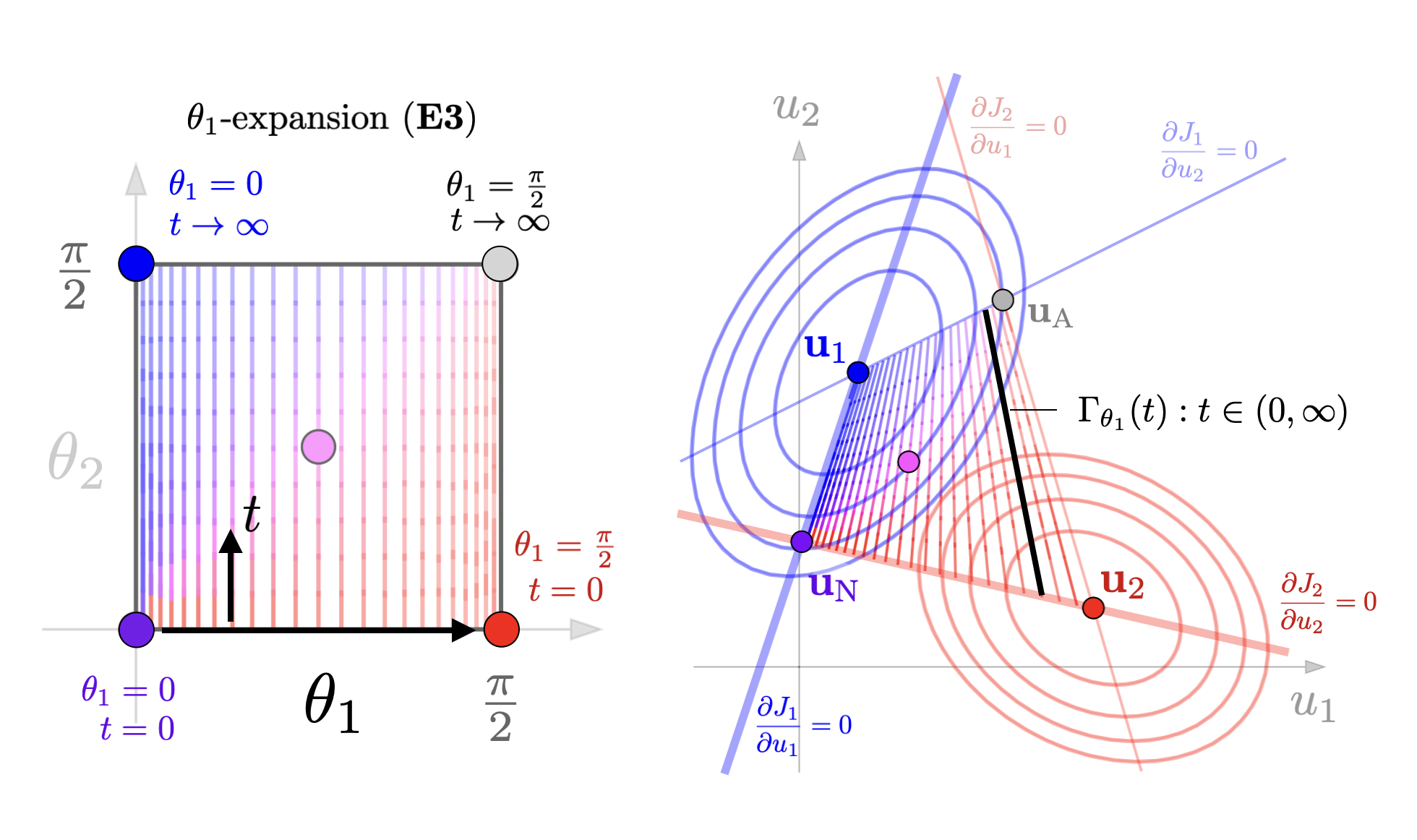
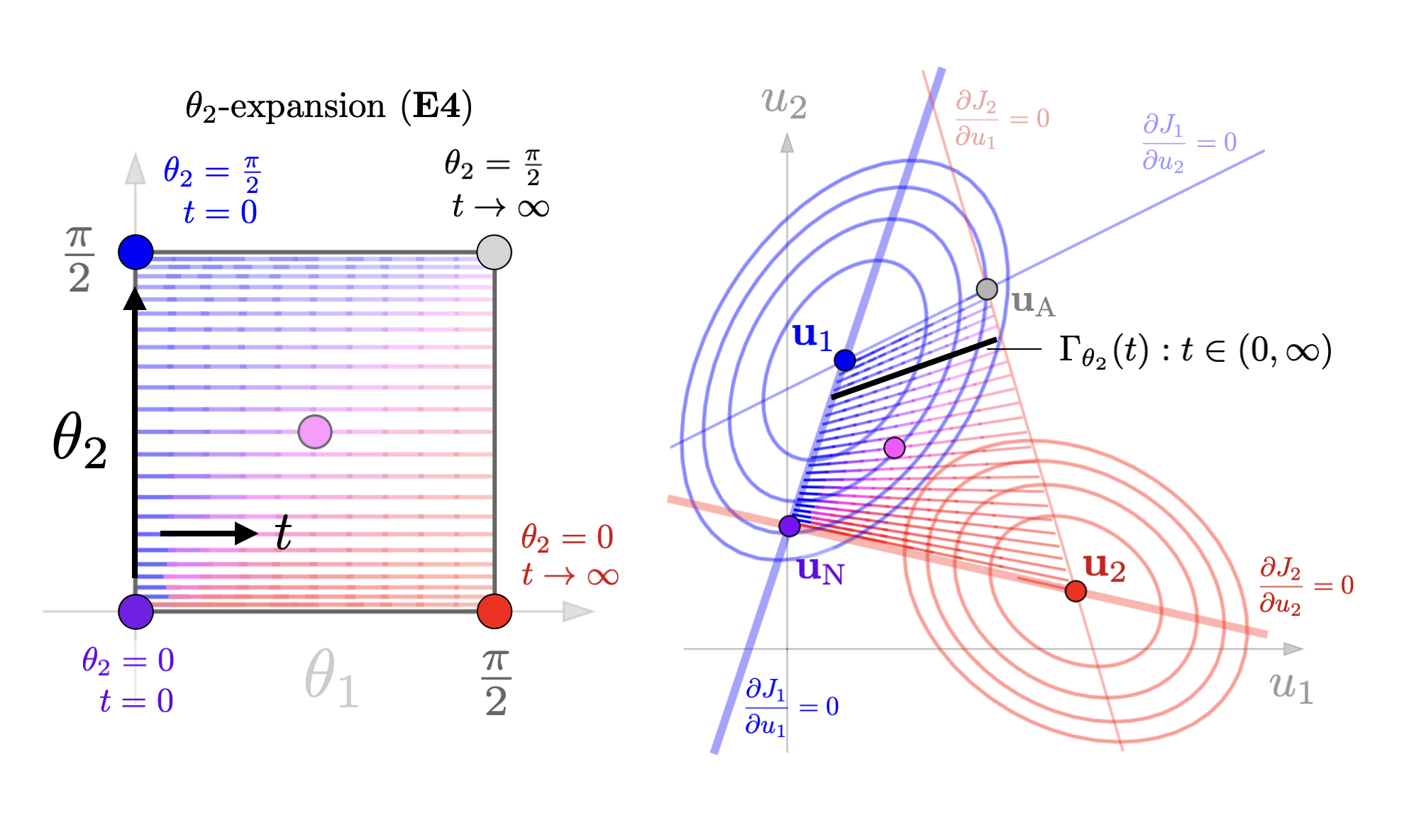
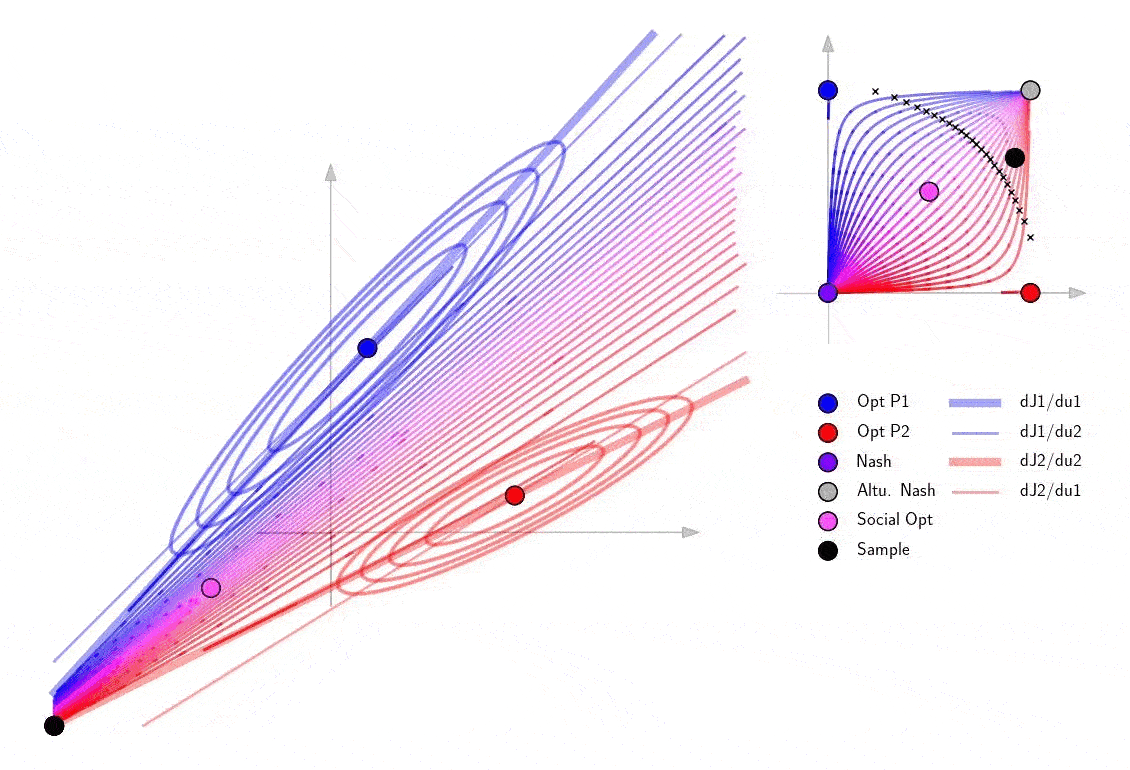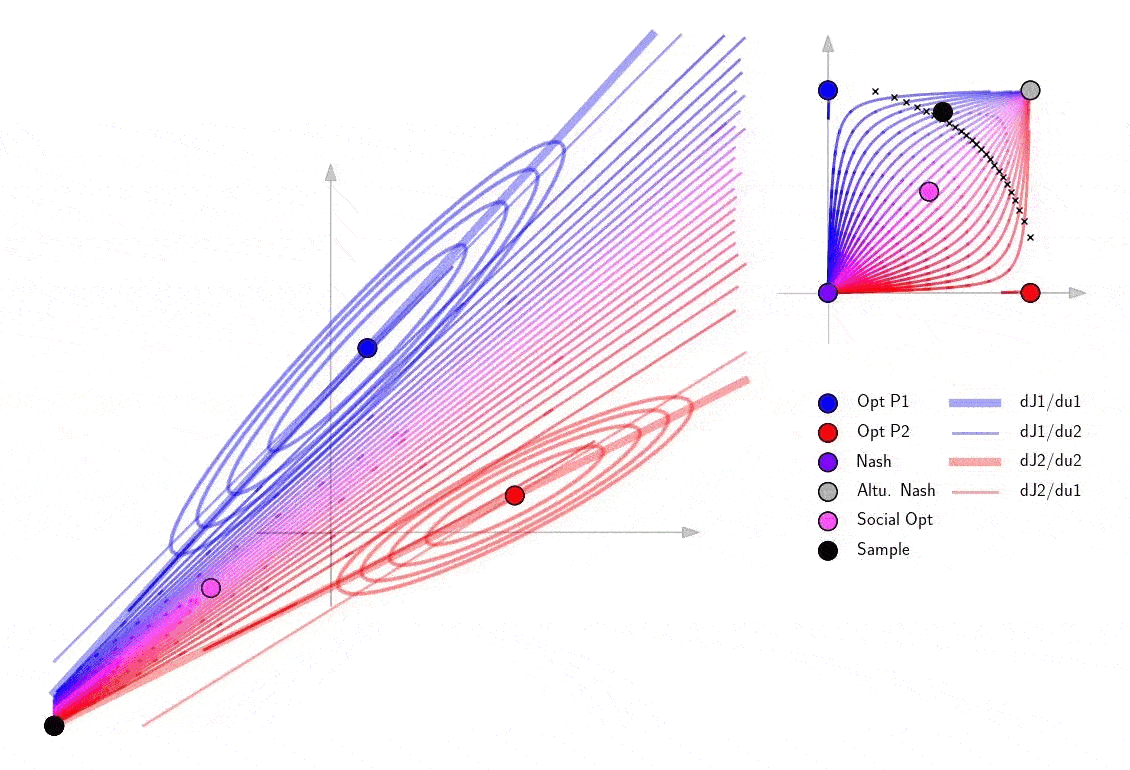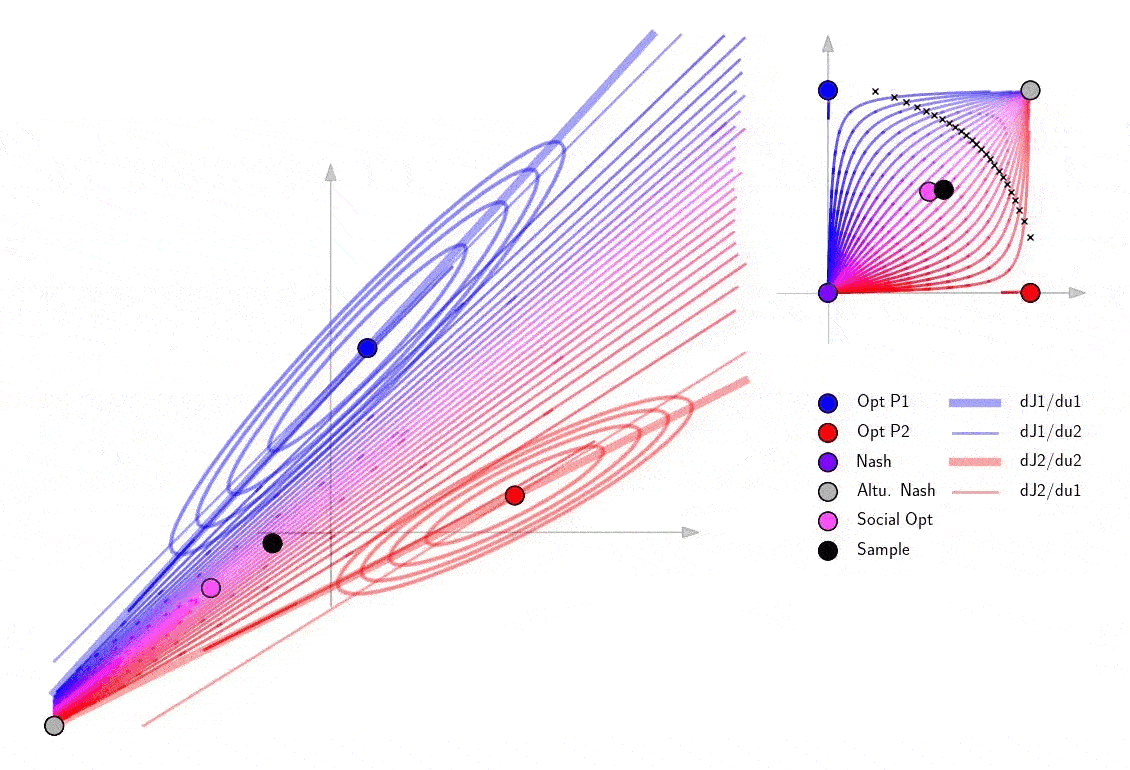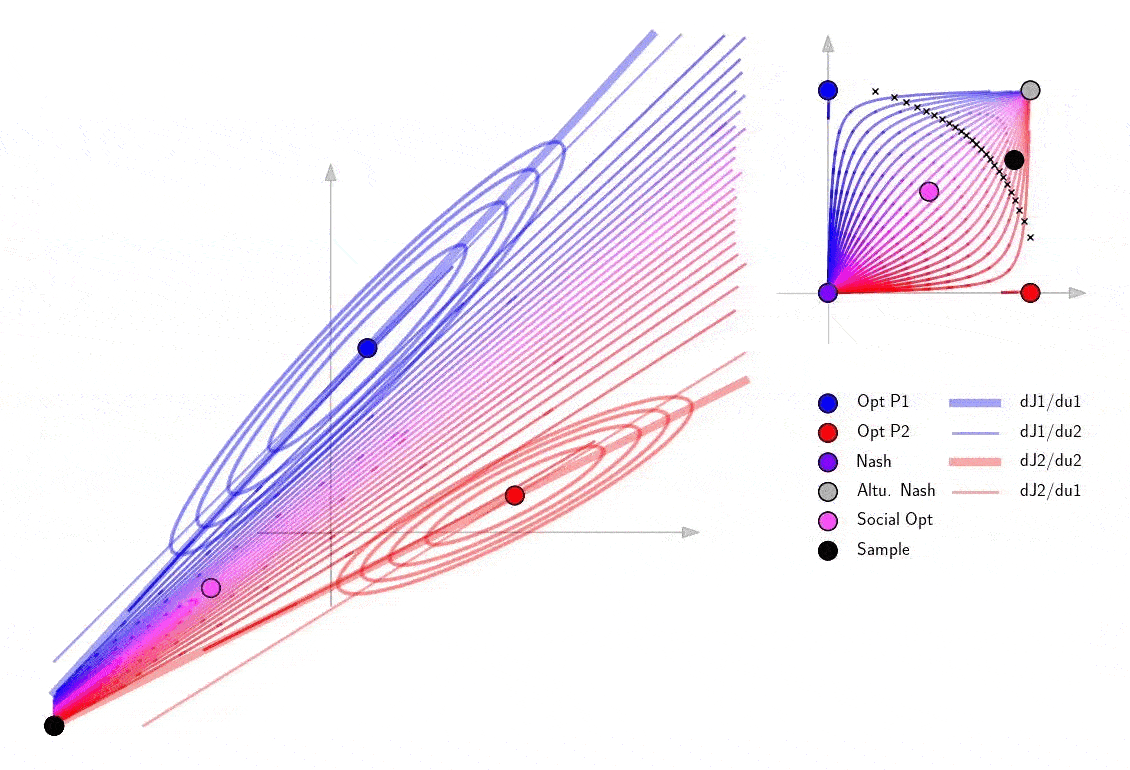
The following example of a 3D joint action space \(u=(u_1,u_2) \in \mathbb{R}^3\) is a good illustration of how the set of SVO Nash equilibria is not in the convex hull of the corner equilibrium points and also not necessarily flat in higher dimensions.

The following figures illustrate the ellipsoidal bounds in the bounded equilibrium case. Note that the shapes of ellipses change for different curves parametrized by \(\phi\) and \(\psi\).

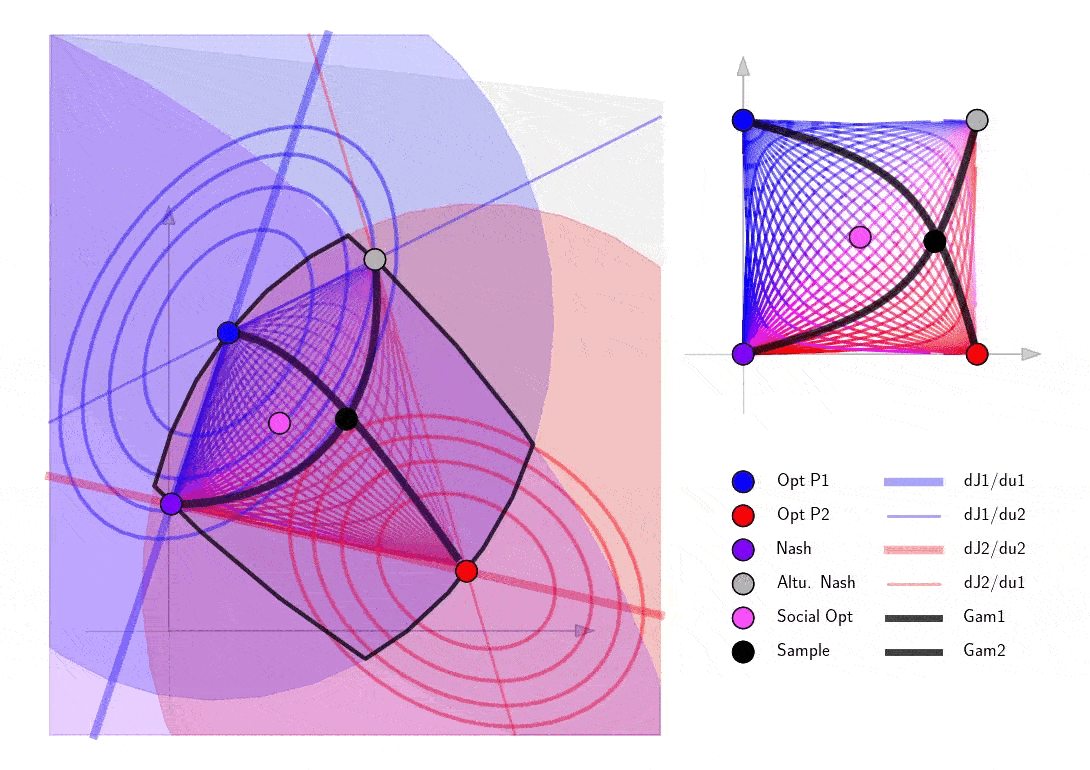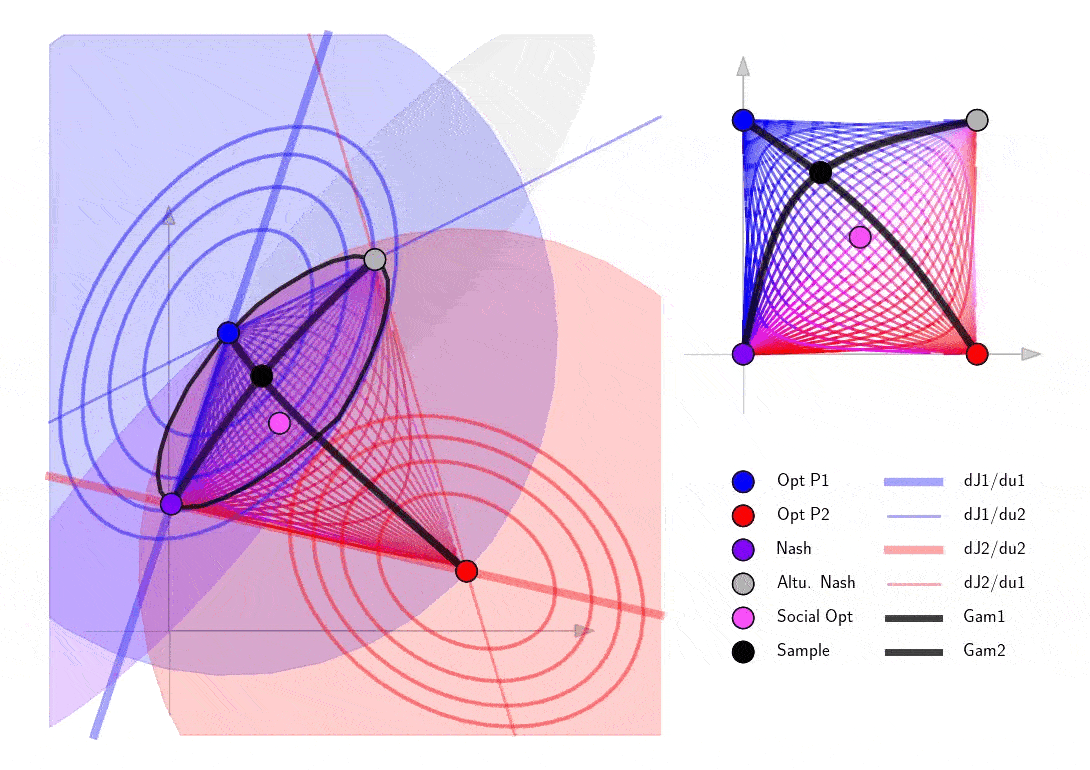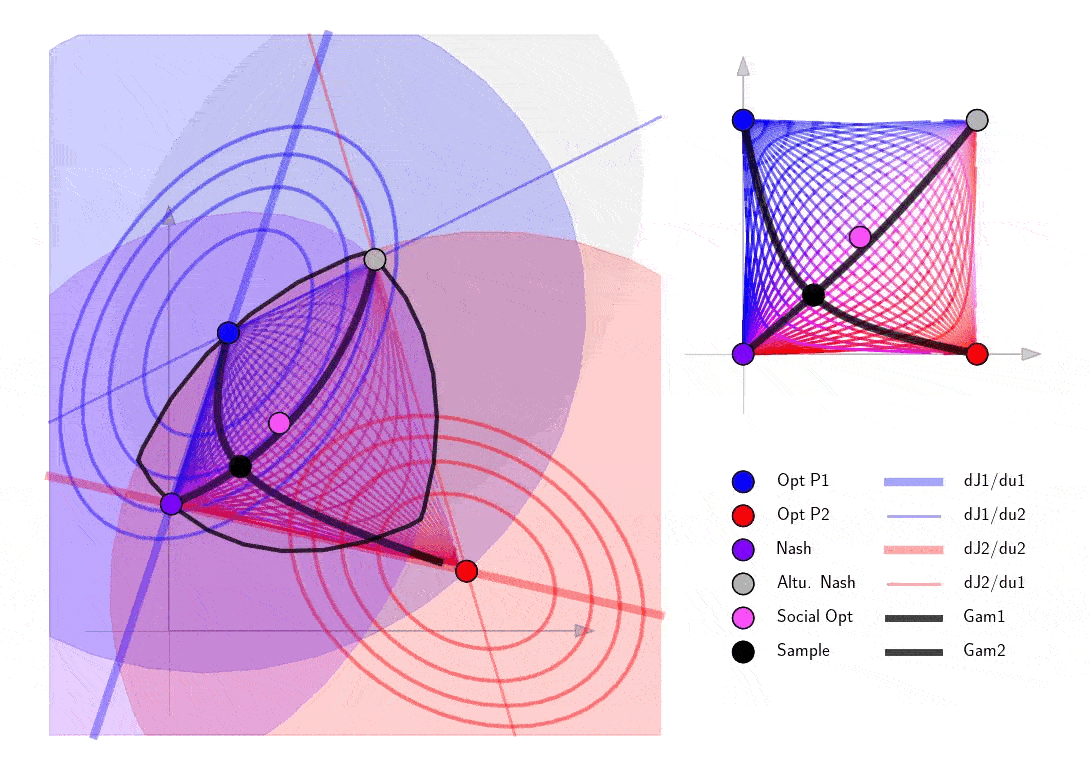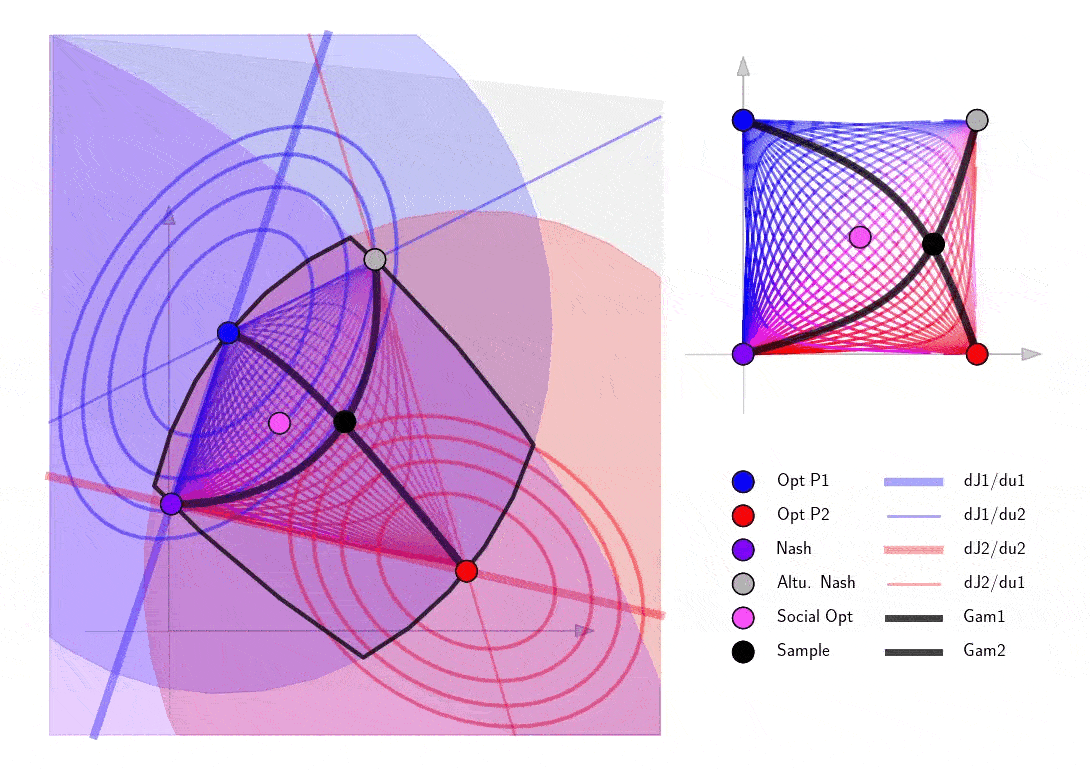
Finally explore the structure of the blow-up points in a 2D example. Note that as the sample cooperation point passes the curve of blow up points, it passes through infinity in the 2D action space and shows up on the other side of the action space.