ABOUT:

I'm a post-doctoral researcher and lecturer at University of Washington under Lillian Ratliff and Behcet Ackimese. My research is in control theory and optimization applied to complex cyber-physical systems involving competition. I am also passionate about teaching and math visualization. I have recently been working on a suite of web-based interactive visualizations for teaching linear algebra, optimization, control theory, and estimation. Further info: visualizations

Contact: dan dot j dot calderone at gmail dot com

Trajectory Planning via Successive Convexification (SCVX):

Successive convexification (or sequential convex programming) can be a powerful tool for trajectory planning in contexts with obstacles and nonlinear dynamics. In this post, we show how SCVX can be applied to solve a basic path planning problem in 2D and 3D spaces.

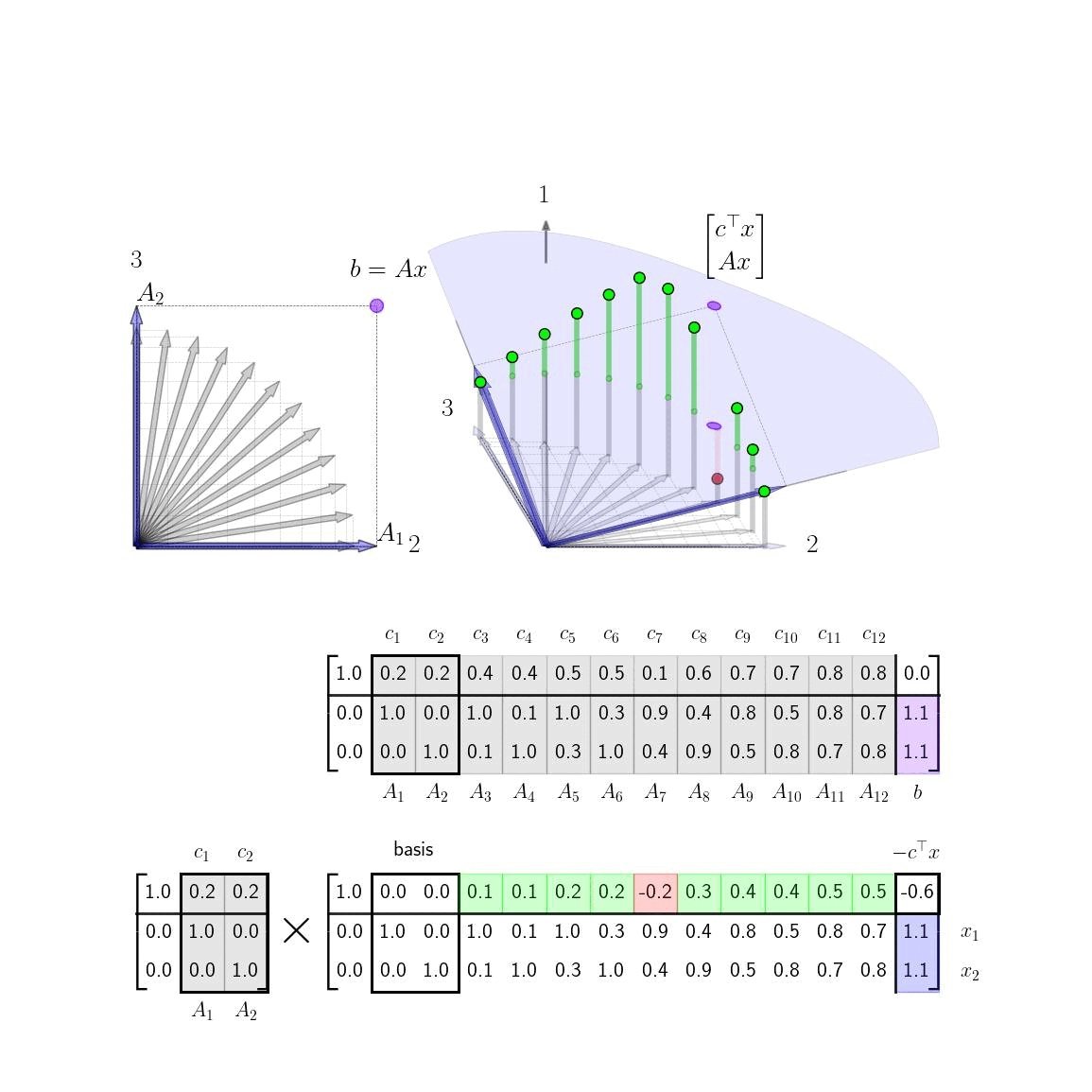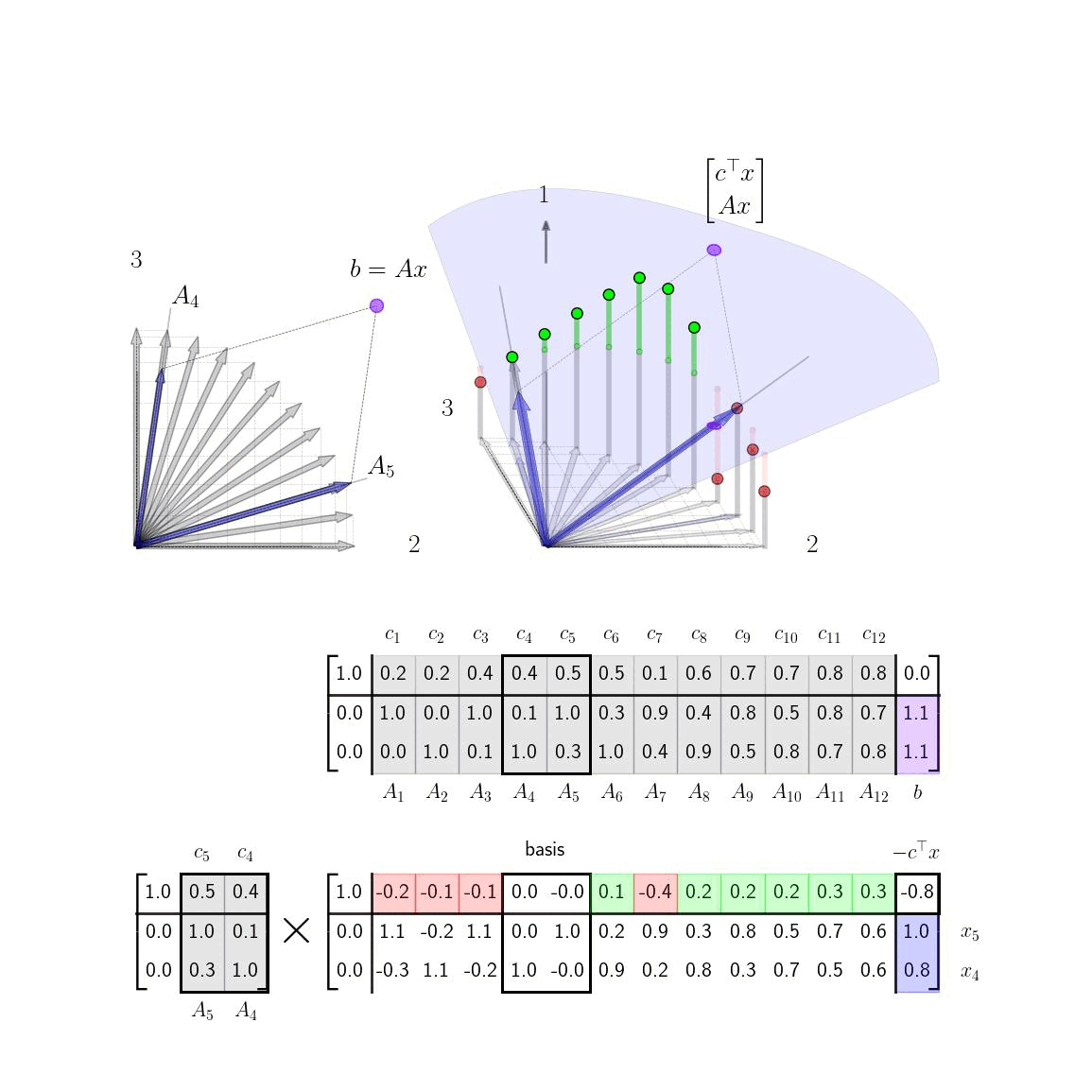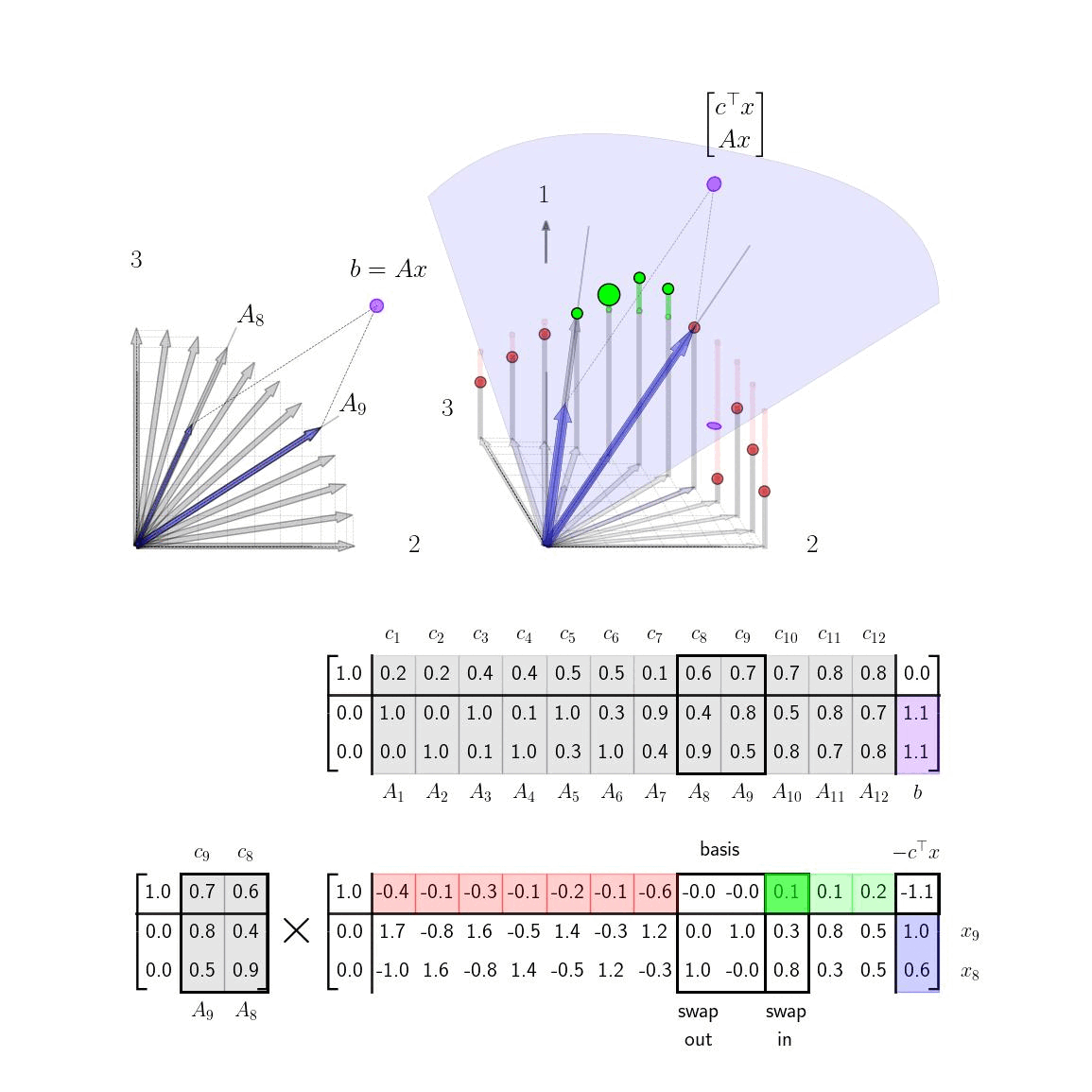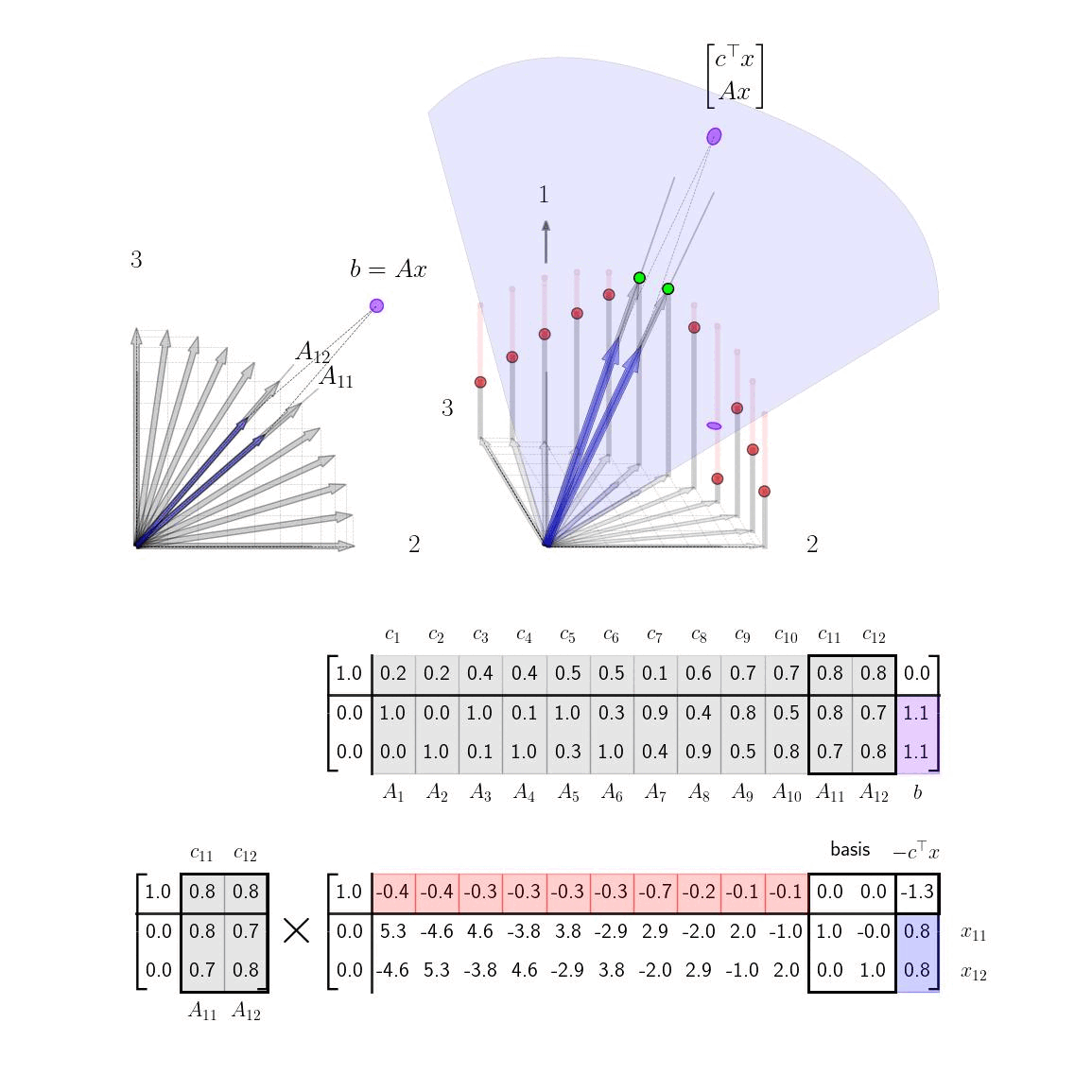
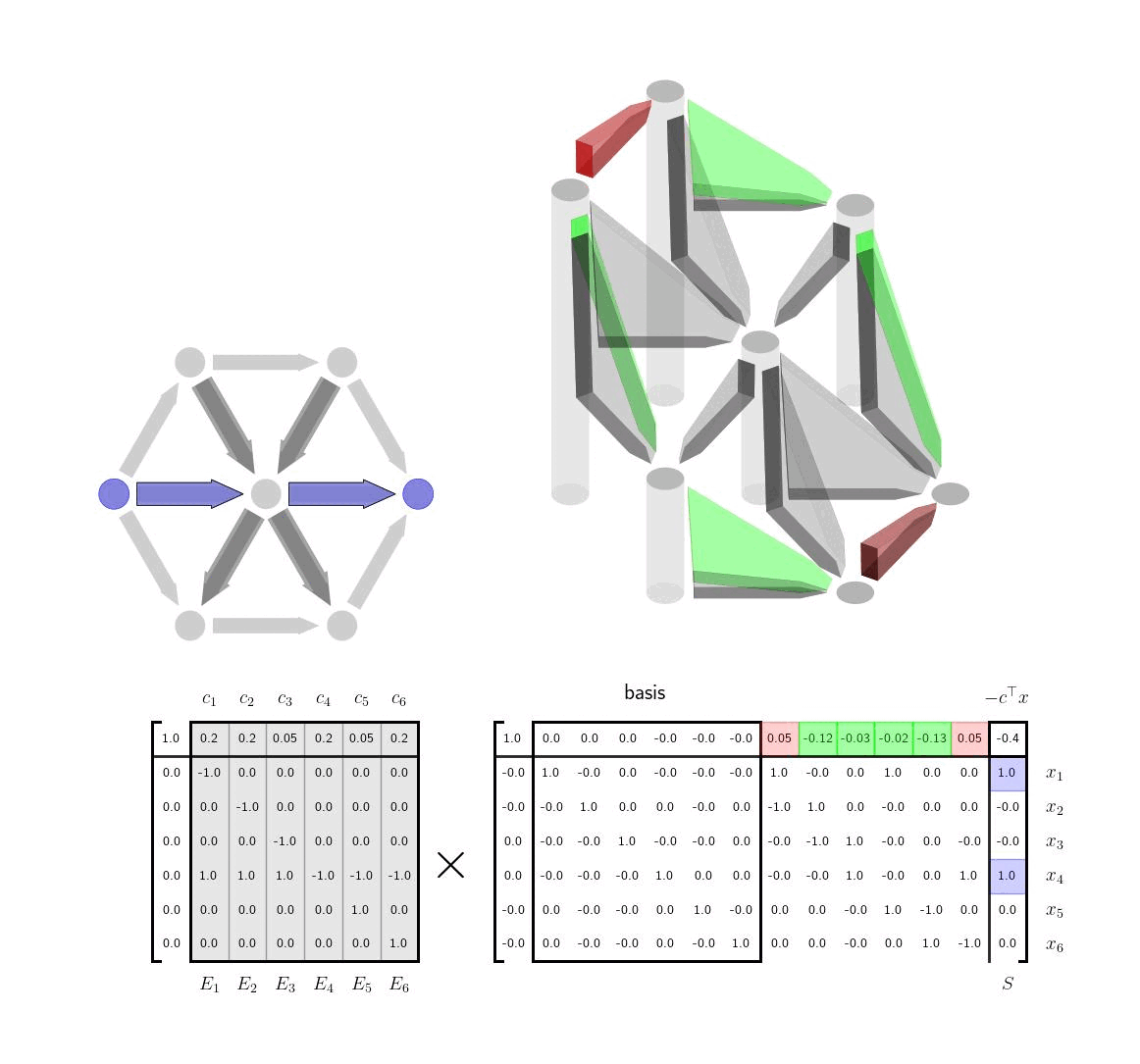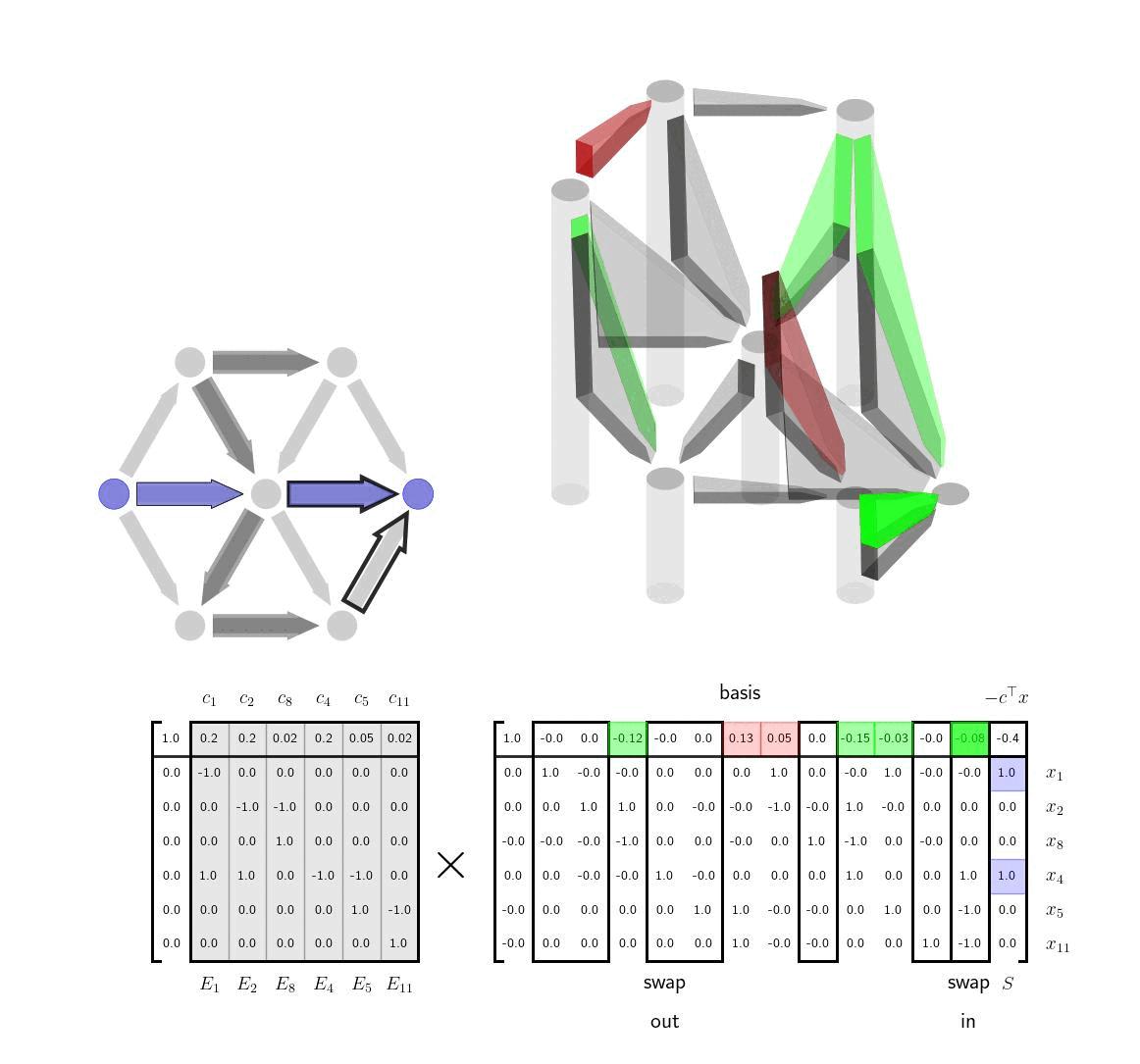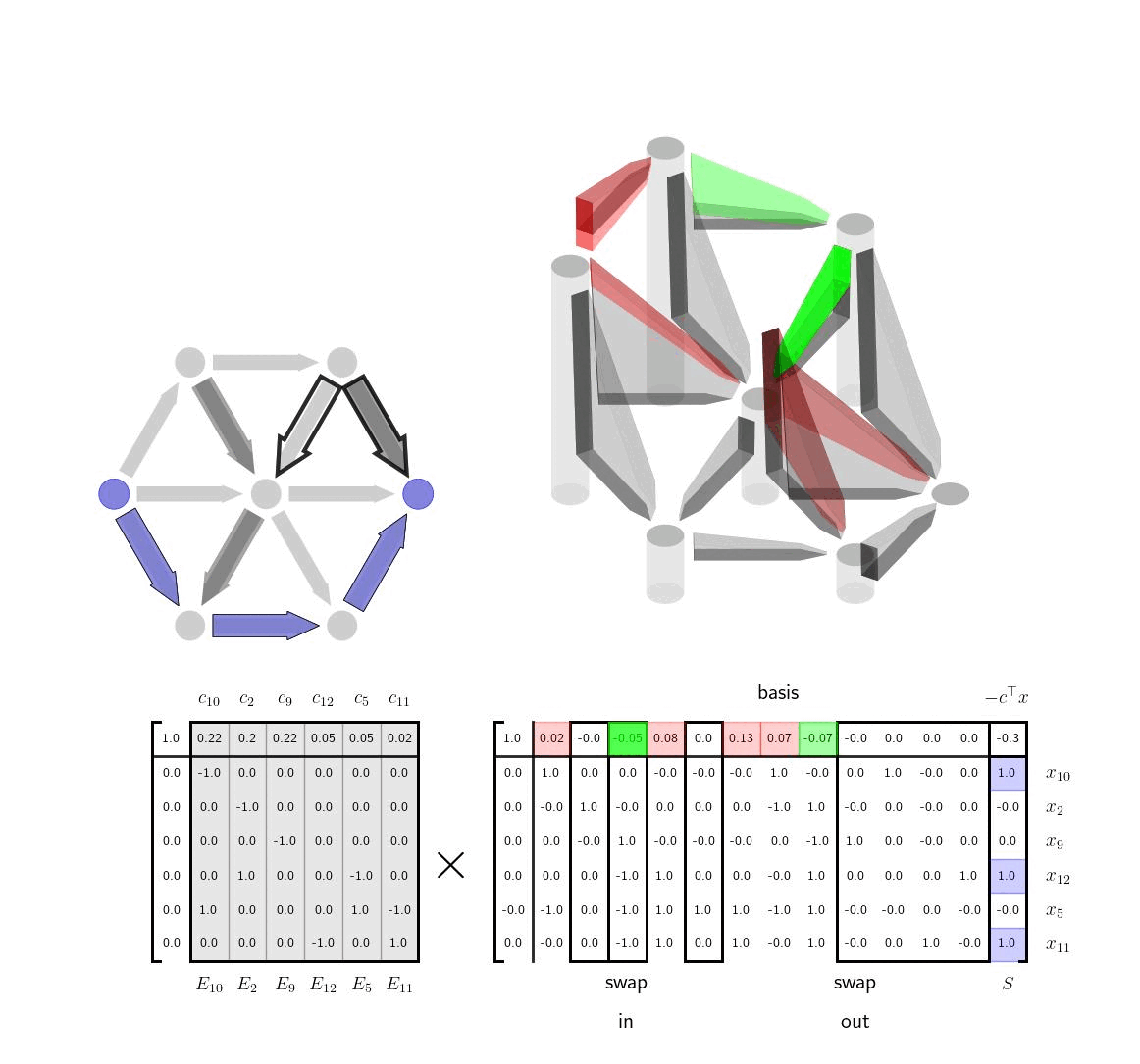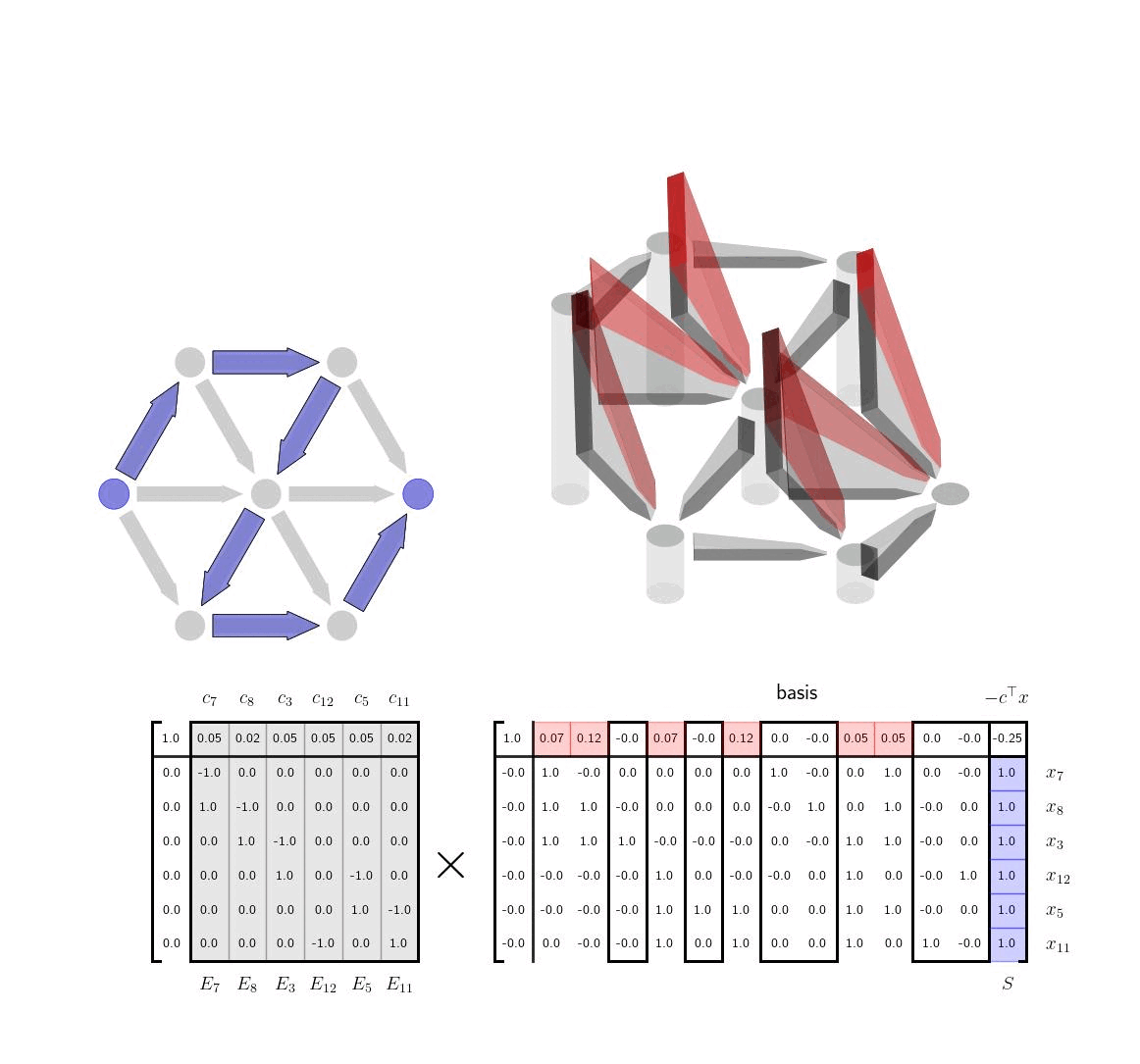
Simplex Method Visualizations

Visualizing the column geometry of the simplex method can provide clear insight into how the algorithm works and also help visually inclined practitioners remember how to implement it.

Shortest Path via the Simplex Method

In this post, we apply the simplex method to solve shortest LPs and give visualizations and interpretation of each step.

Vector Shapes:

Here we show the geometry of various vector shapes in up to 8-dimensions in an orthogonal and parallel axis representation. The vector snaps to the various shapes as you drag it.

The right slider changes the shape being displayed. Clicking the lock symbol on the vector allows the vertical slider to go beyond 4-dimensions.

Further info: Vector Sets

Vector Addition:

Vectors can be visualized relative to an orthogonal axis or with the coordinates represented in parallel. In this visualization, we show vector addition in both the orthogonal axis and parallel axis representation. In the orthogonal axis case, vector addition can be visualize by connecting the vectors tip-to-tail as shown.

The vectors can each be adjusted manually by dragging the corners of the hypercubes or by the heights of the stacks in the parallel representation. Hover and click on the vector elements to highlight them. The right-top slider on the equation allows some vectors to be hidden; the clicking hte "lock" symbols and dragging down the vertical slider increases the dimension of the vectors shown up to 8-dimensions.

Further info: Vector Addition