danjcalderone

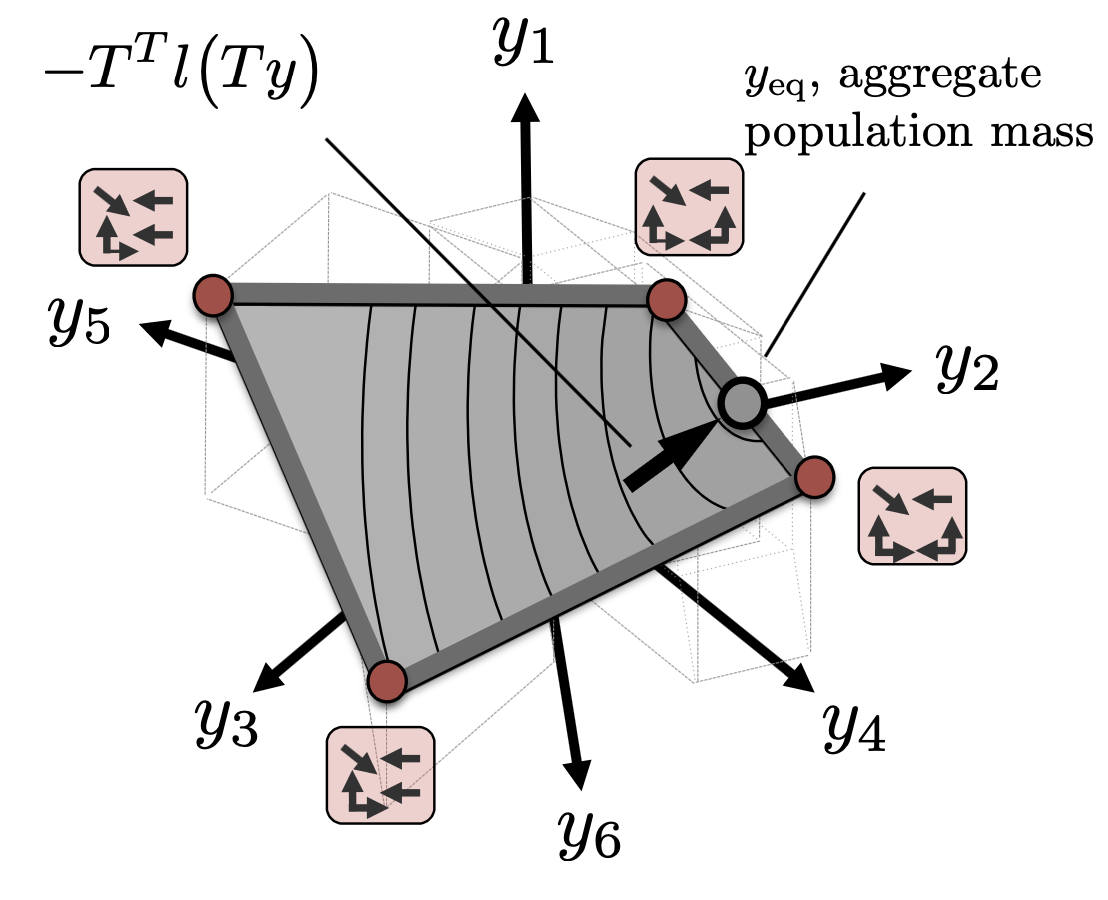
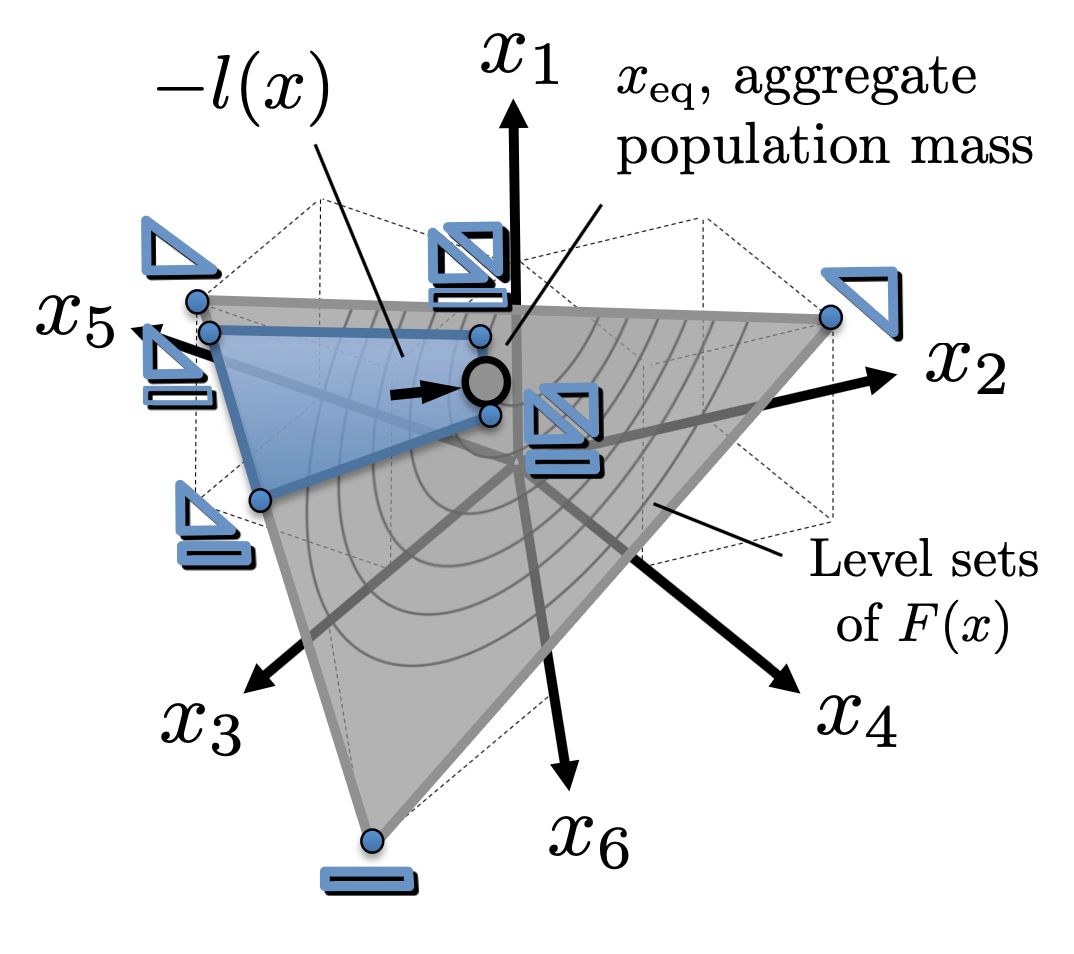
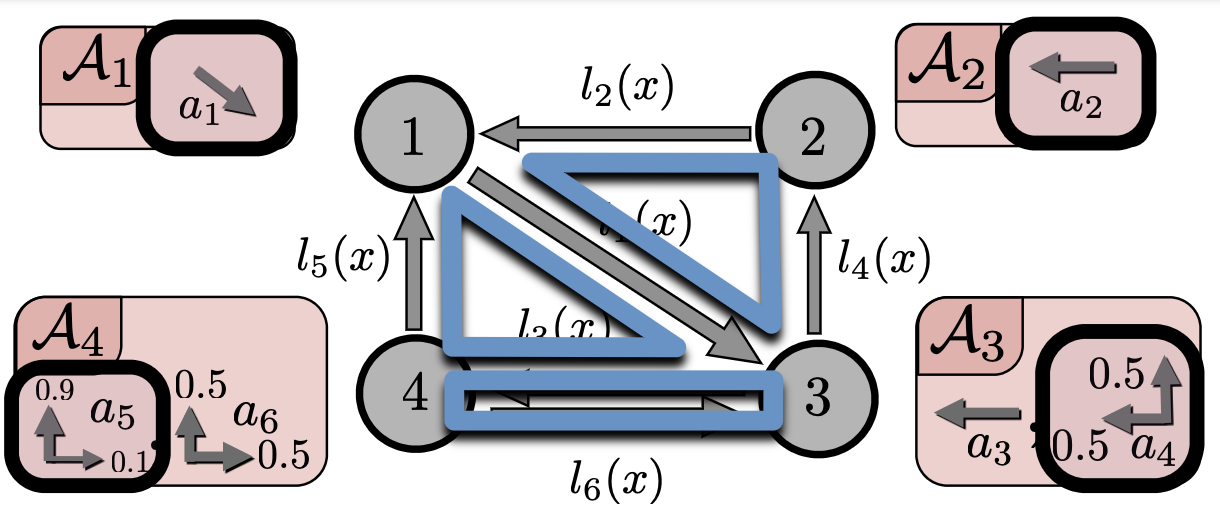
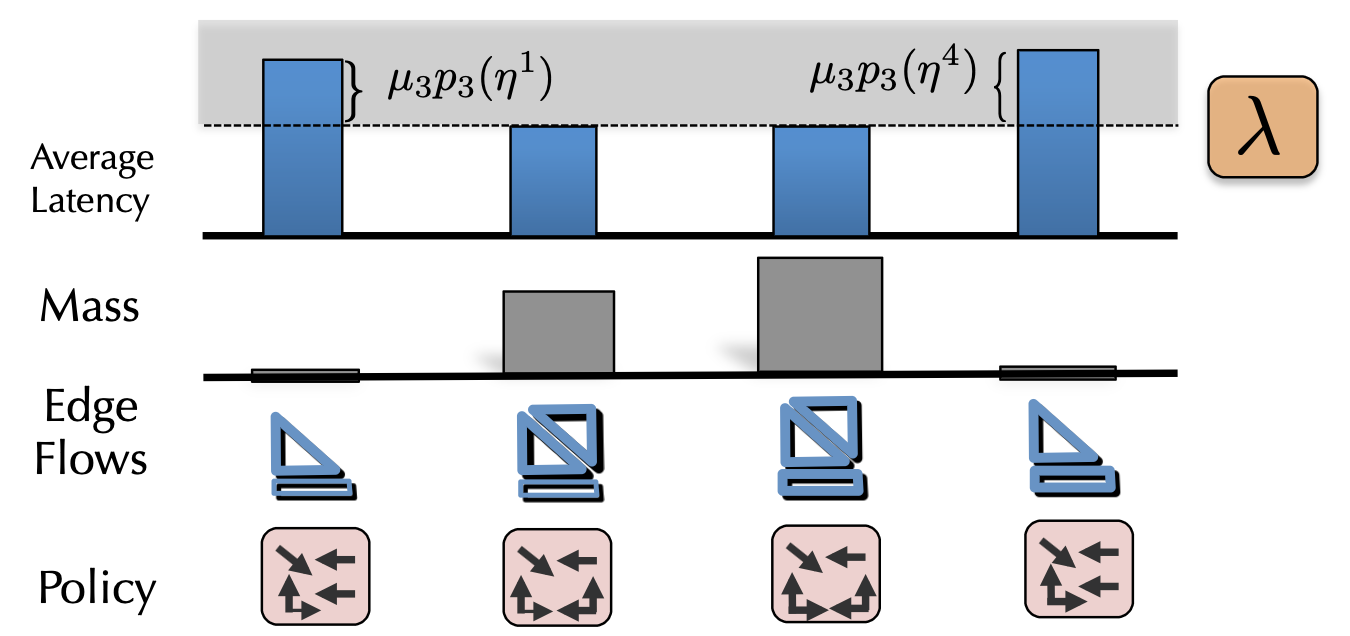
Topical-Index, Alphabetic-Index,

Collected

• Linear Algebra: linalg(lec),

Basics

• Block-matrix multiplication: block(slides), block(web),

Complex Analysis

• Complex Numbers: complex(lec),

Calculus

• Derivatives: derivs(lec), derivs(web),
• Linearization: lin(slides),
• Product Rule: calc(slides),
• Integration by Parts: calc(slides),
• Leibniz Integral Rule: calc(slides),

Vectors

• Vectors/Vector sets: vecs(mono), vecs(web), vecsets(web), vecadd(web),
• Subspace:
• Linear combinations: combs(lec), lincombs(web),
• Span: span(lec),
• Positive combinations: combs(lec),
• Convex combinations: combs(lec), cvxcombs(web),
• Norms: matprod(lec), norms(web),
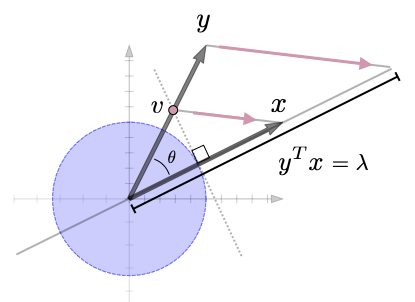
• Inner products: matprod(lec), inner(lec), inner(web), outer(web),

Matrices

• Linear transformations: lintrans(web),
• Column geometry: cols(mono), colrow(slides), cols(slides), fundthm(slides), colrows(web),
• Row geometry: colrow(slides),
• Transposes:
transpose(web),
• Matrix Addition: matadd(slides), matadd(web),
• Matrix Multiplication: matmult(slides), matmult(web),
• Matrix Norms: matnorms(web),
• 2x2 Matrices: 2x2(mono),

Bases & Coordinates

• Bases: bases(web),
• Coordinates: coords(lec), coords(web),
• Orthogonality:
• Orthonormal transformations: ortho(web),
• Orthonormalization: orthonormal(web),
• Rotations: rotations(lec), rotations(slides),
• Inverses: invs(lec), invs(web), inv(ref),
• Similarity Transforms: sim(web),
• Congruent Transforms: cong(web),
• Projections: projs(lec), projs(web),

Fundamental Theorem

• Range space: range(web),
• Nullspace: nullspace(web),
• Matrix Rank/Rank-Nullity: ranknull(web),
• Fundamental Thm (linear algebra):
• System of Eqns:
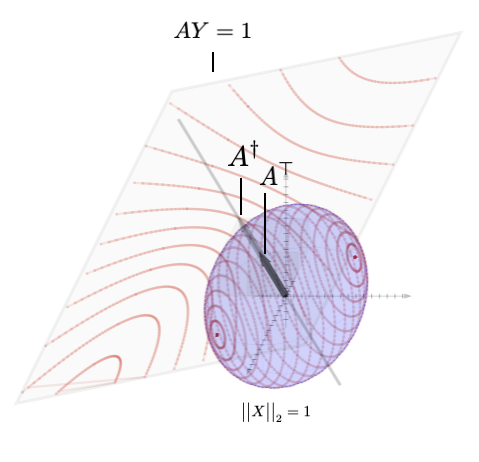
• Pseudo-inverses: pinvs(web),
• Left-Right Inverses: lrinvs(web),
• Gaussian Elimination: gausselim(web),
• Elementary matrices: gerows(slides), gecols(slides),

Eigenvalue Decomposition

• Diagonalization: eig(slides),
• Eigenvalues/Eigenvectors: eig(slides),
• Characteristic polynomial: eig(slides),
• Spectral mapping theorem: eig(slides),

Singular Value Decomposition

• Polar decomposition: decomps(lec), svd(slides),
• Singular Value Decomposition: decomps(lec), svd(slides),

Signal Processing

• Discrete Fourier Transforms: dft(slides),

Modeling

• Kinematics: kinematics(slides),
• Mechanics: dynamics(slides),
• Circuits: circuits(slides),

Linear Systems

• Ordinary Differential Eqns (ODEs): odes(lec),
• Linear systems: ltisys(slides),
• Controllability: ltisys(slides), ctrlobs(slides),
• Observability: ltisys(slides), ctrlobs(slides),

Control Theory

• Controls:
• Disturbance Rejection: disturbs(slides),
• MIMO control:
• Uncertainty modeling: lfruncertainty(slides),

Estimation Theory

• Estimation: kfs,
• Kalman filters: kfvis(slides), kf(ref), kfexamples(ipynb),

(Algebraic) Graph Theory

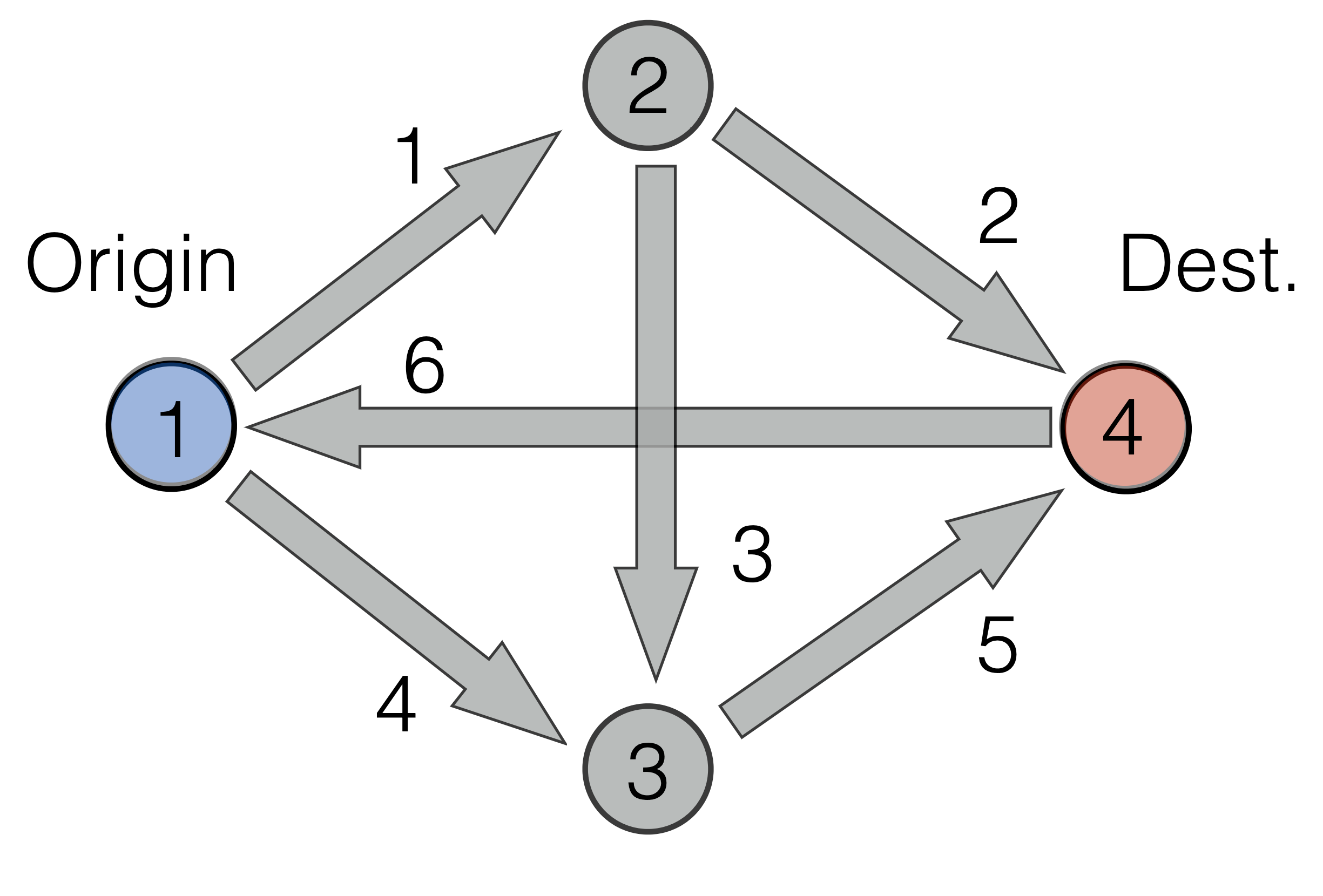
• Graph theory:
• Algebraic graph theory: graphflows(mono), graph(slides), treescycles(blog),
• Laplacians: graph(slides),
• Adjacency Matrices: graph(slides),
• Incidence matrices: graph(slides), treescycles(blog),

Markov Decision Processes

• Markov decision processes: mdps(mono), mdps(slides),

Data Science

• High dimensional inner products: highdim(slides),
• Regression: regress(slides),
• Classification: classify(slides),

Algorithms

• Algorithms: algos(slides),
• Arrays: arrays(slides),
• Python: python(slides),

Drawing

• Drawing: drawing(slides),

Convex Optimization

• Affine spaces: affine(slides),
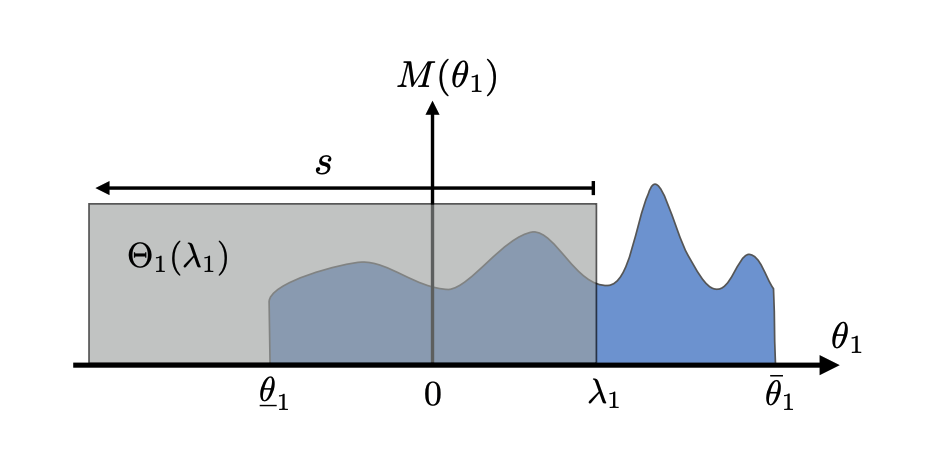
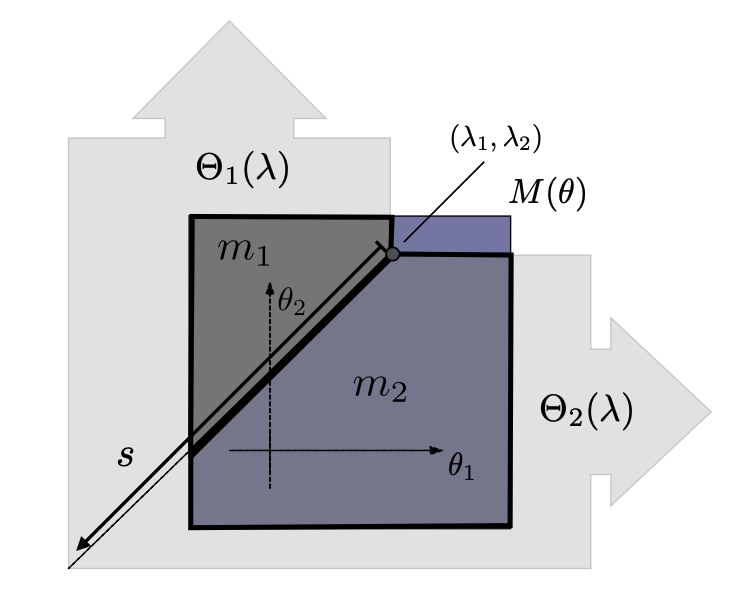
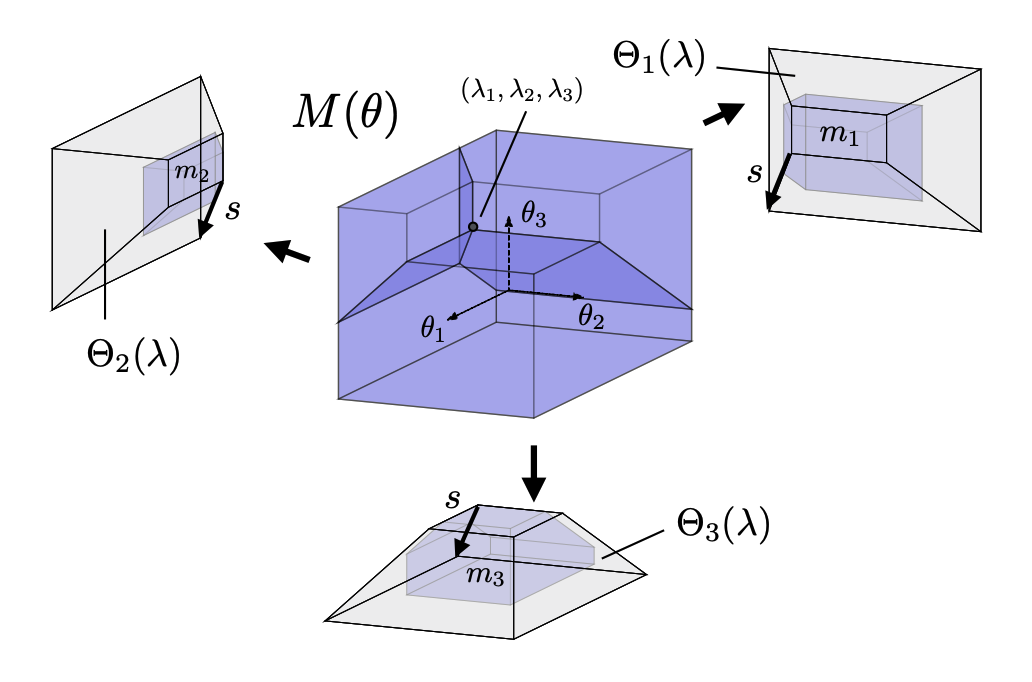
• Polytopes: polytope(mono),
• Pos & Neg (semi-)definite: posdef(slides), svd(slides),
• Quadratic forms: posdef(slides),
• Congruent Transforms: cong(web),
• Duality: duals(slides),
• Linear programs (LPs): duals(slides),
• Quadratic programs (QPs): duals(slides),
• Second order cone programs (SOCPs): duals(slides),
• Semi-definite programs (SDPs): duals(slides),
• KKT Conditions kktmat(slides),
• KKT Sensitivity kktsens(slides),
• Simplex Method simplex(ipynb), simplex(ex), simplex(blog), simplexroute(blog),
• Bipartite Matching bipartite(slides),
• Successive Convexification (Trajectory Planning): scvx(blog),