Teaching Interests:
My main teaching interests are in applied linear algebra to various modeling fields including control, optimization, estimation, and machine learning. I have a particular interest in visualization.
My recent and current courses include linear algebra, linear system theory, algebraic graph theory, markov decision processes, classical control theory, multivariable control, estimation theory, convex optimization, robust control, and network dynamics.
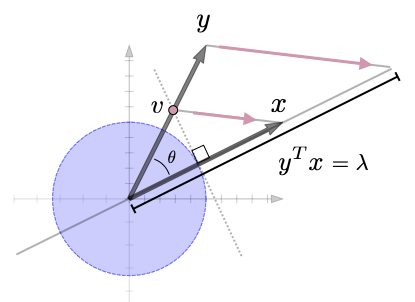
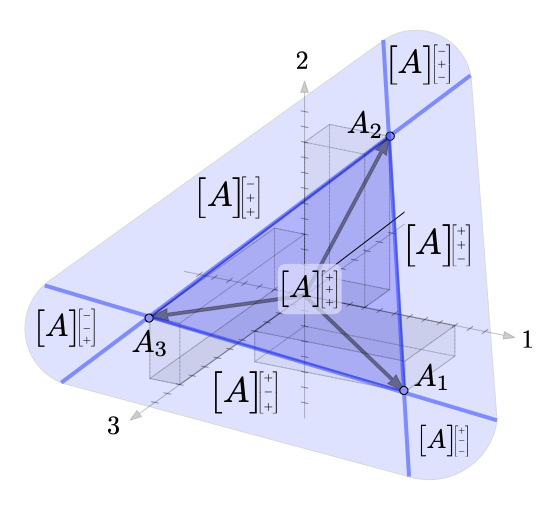
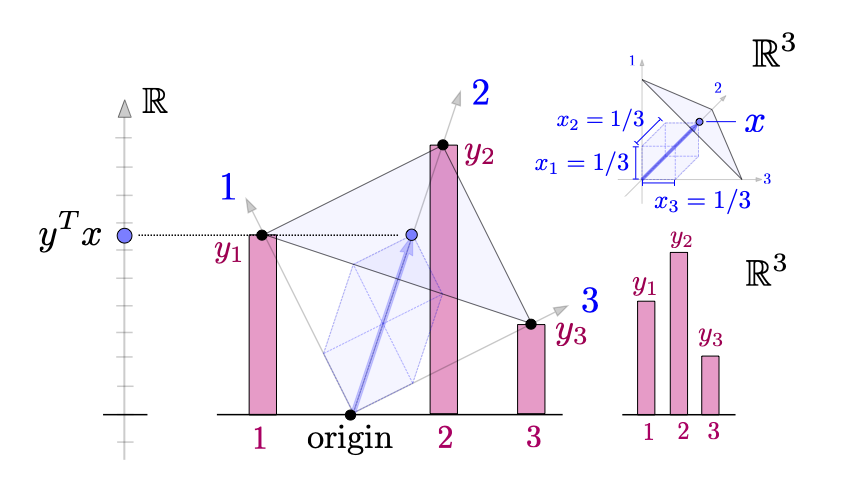
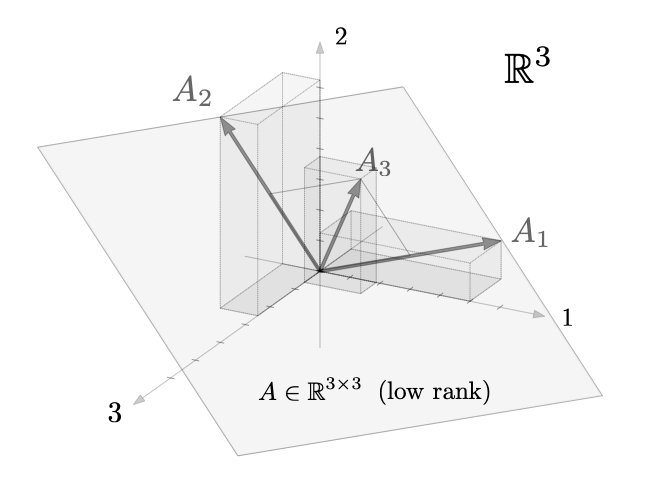
Topical-Index Alphabetic-Index
NOTES:The following are collected linear algebra notes. The topical links are subsections of the full set of notes.
Collected: Linear algebra
Topical:
The following monographs expand on visualization techniques for linear algebra, convex optimization, algebraic graph theory, and Markov decision processes.
SLIDES:
The following are a collection of slides decks on various topics. Each slide deck is quite dense and may be more useful for review than for initial exposition. Many of them use a flip-book pseudo-animation style and should be viewed in a way where the slides can be changed rapidly.
Linear Algebra:
Column Geometry:
Linear Systems:
Convex Optimization:
Network/Graph Theory:
Calculus:
Physics:
Control:
Estimation:
Algorithms
Machine Learning:
Coding:
UW Courses: AA/EE510, AE510
Offerings: Fall20 (AA510), Win20,Win21,Win22 (AE510)
Primary Topics:
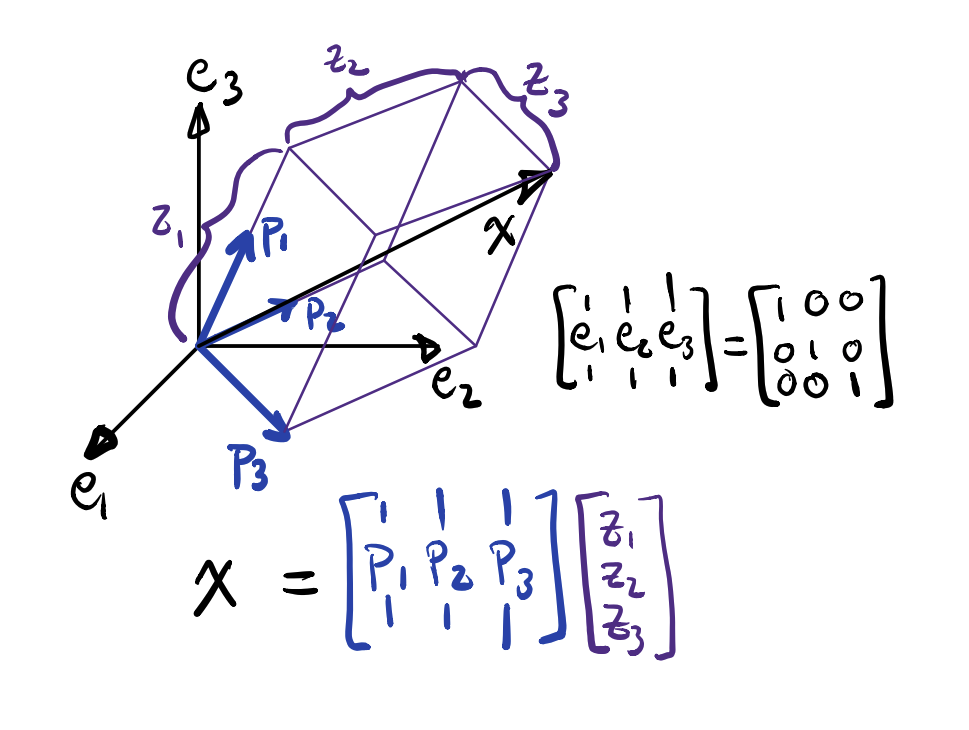
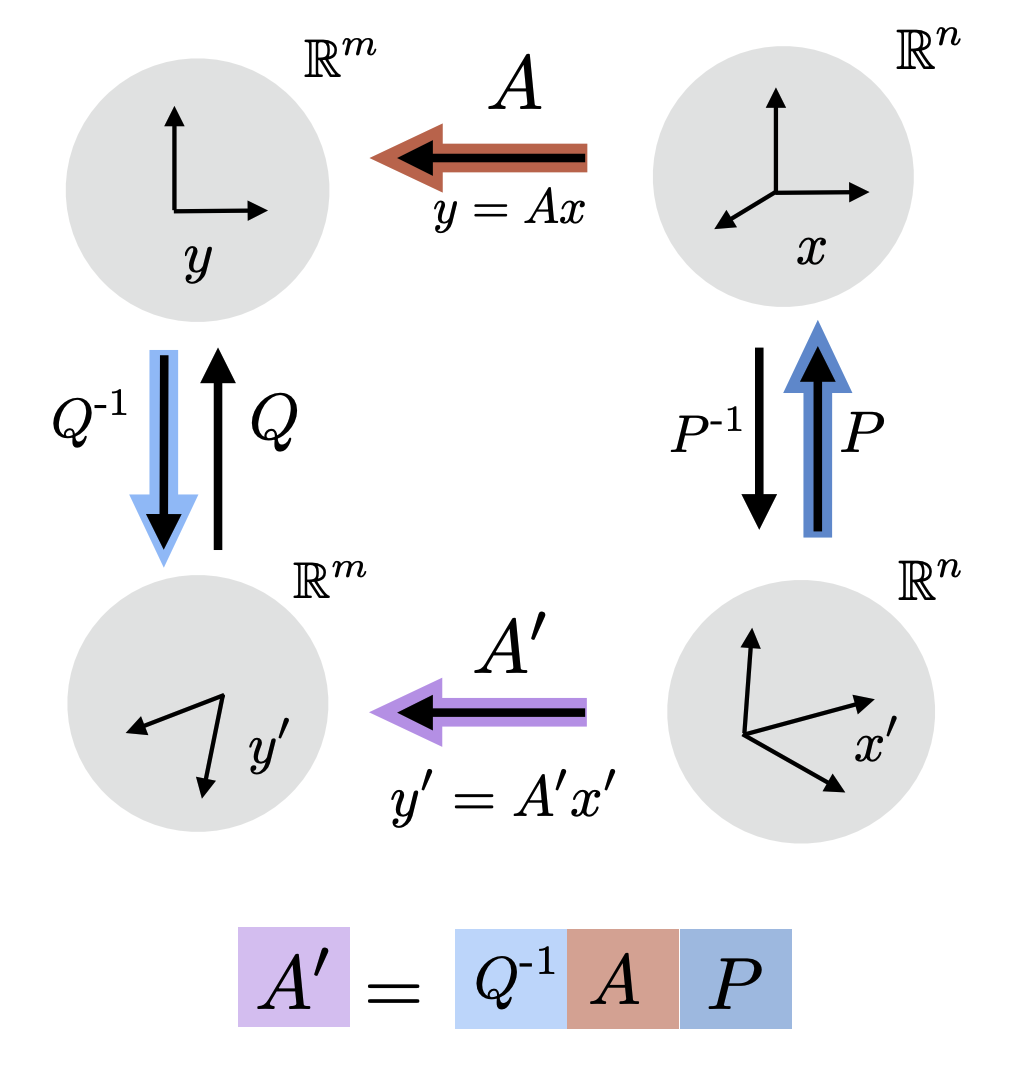
Vectors, inner products, linear transforms, matrices, block mtarices, range/nullspace, rank, fundamental thm, Gaussian elimination, matrix inverses/pseudo-inverses, systems of equations, coordinate transforms, similarity transforms, eigenvalues/eigenvectors, diagonalization/Jordan form, spectral mapping, Cayley Hamilton, traces/determinants, matrix exponential, state-space models, LTI/LTV systems, ODE solutions, Laplace transforms/transfer functions, controllability, observability, controllable canonical form, feedback design & pole-placement, observer design, separation principle, Grammians, singular value decomposition, polar decomposition.
Syllabus: syllabus
Class notes:
Fall20: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8 lec9 lec10 lec11 lec12 lec13 lec14 lec15 lec16 lec17 lec18 lec19 lec20
Win21: lec1 lec2 lec3 lec4 lec5 lec6 lec7a lec7b lec8 lec9 lec10
Homeworks:
Win20: hw1 hw2 hw3 hw4 hw5 hw6 hw7 hw8
UW Courses: AA447
Offerings: Spr21
Syllabus: syllabus
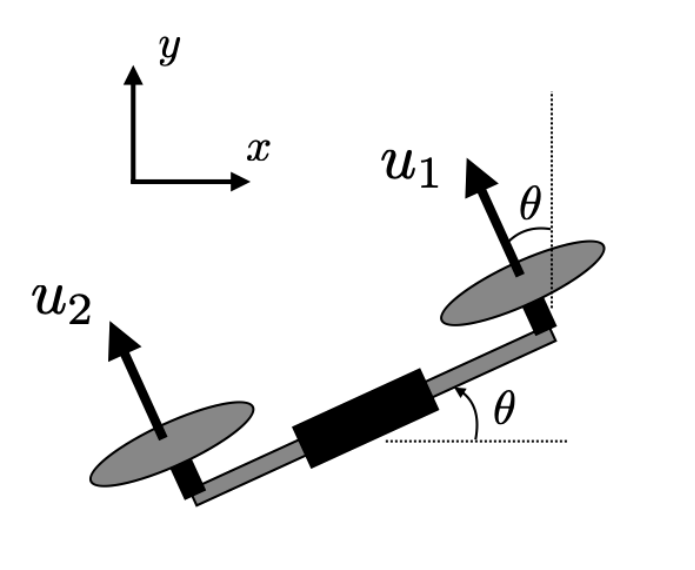
Topics: Time & frequency domains, Laplace transforms, state space models & transfer functions, impulse responses and convolutions, system modeling,block diagrams, PI/PID control, disturbance rejection, internal model principle, Bode-plots, Nyquist plots, Nyquist stability criteria, gain/phase/stability margins, loop transfer functions, loop shaping principles.
Class notes:
Spr21: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8 lec9 lec10 lec11 lec12 lec13 lec14 lec15
Homeworks:
``
UW Courses: AE513
Offerings: Fall19,Fall21
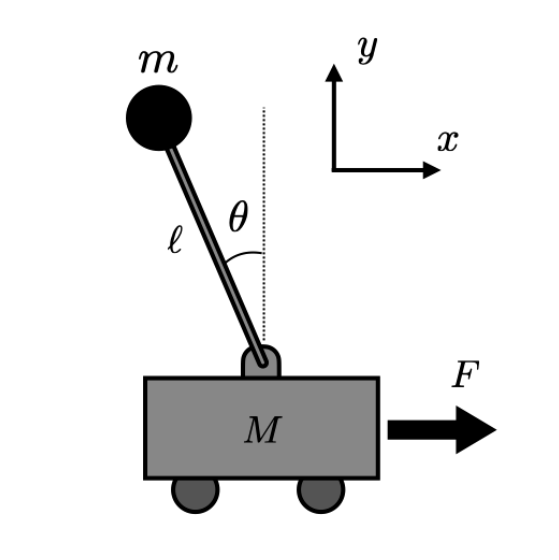
Topics: Dynamical systems (LTI/LTV/nonlinear), linearization (around equilibria and trajectories), open-loop and feedback control, Postive definite matrices, Lyapunov theory, Lyapunov operators - structure and solutions, Grammians, dynamic programming, Bellman equation, linear quadratic regulator (LQR) (for DT & CT, fin & inf horizon), Riccati ODEs, algebraic Riccati equations, solutions through Hamiltonian systems, connections to block matrix eigenvalue problem (advanced), least squares (application to LQR), adjoint method for nonlinear programming (application to LQR), state and costate equations, gradient descent for optimal control output feedback, observer design & separation principle, introduction to Kalman filters, linear quadratic Gaussian (LQG) control.
Class notes:
Fall19: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8 lec9 lec10
Fall21: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8 lec9 lec10
Homeworks:
UW Courses: AA549,AE514
Offerings: Spr19,Spr21(549); Fall20(514)
Topics: Positive definite matrices, basic probability, multivariate Gaussians, covariance matrices, basis functions, weighted least squares, nonlinear least squares, maximum likelihood estimation (MLE), maximum a-posteriori estimation (MAP), Kalman filter (CT & DT), extended Kalman filter, unscented Kalman filter, particle filters
Class notes:
Fall20: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8
Spr21: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8 lec9 lec10 lec11 lec12 lec13 lec14
Homeworks:
Spr21: hw1 hw2 hw3 hw4 hw5 hw6 hw7
Supplemental:
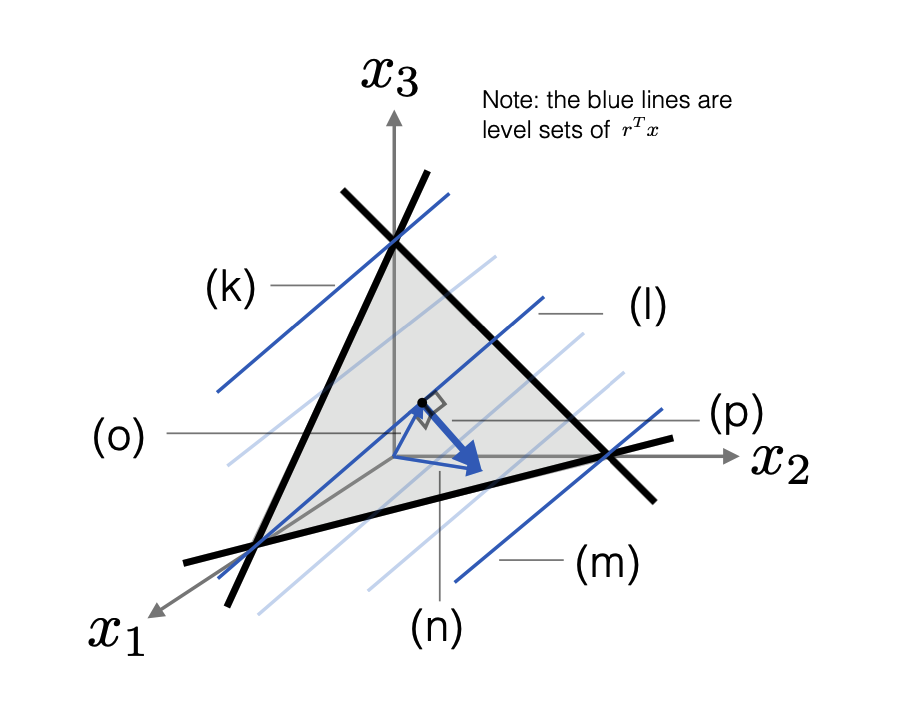
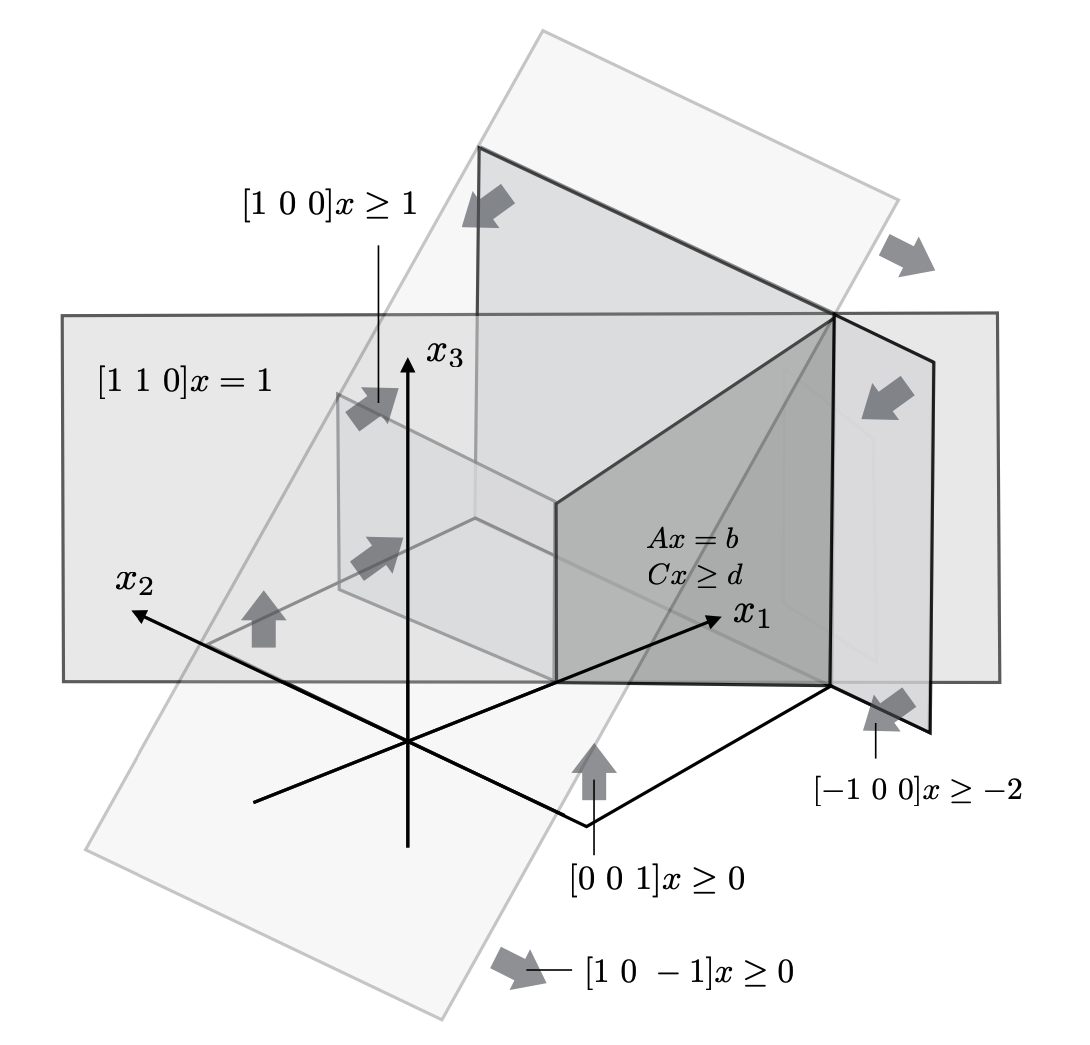
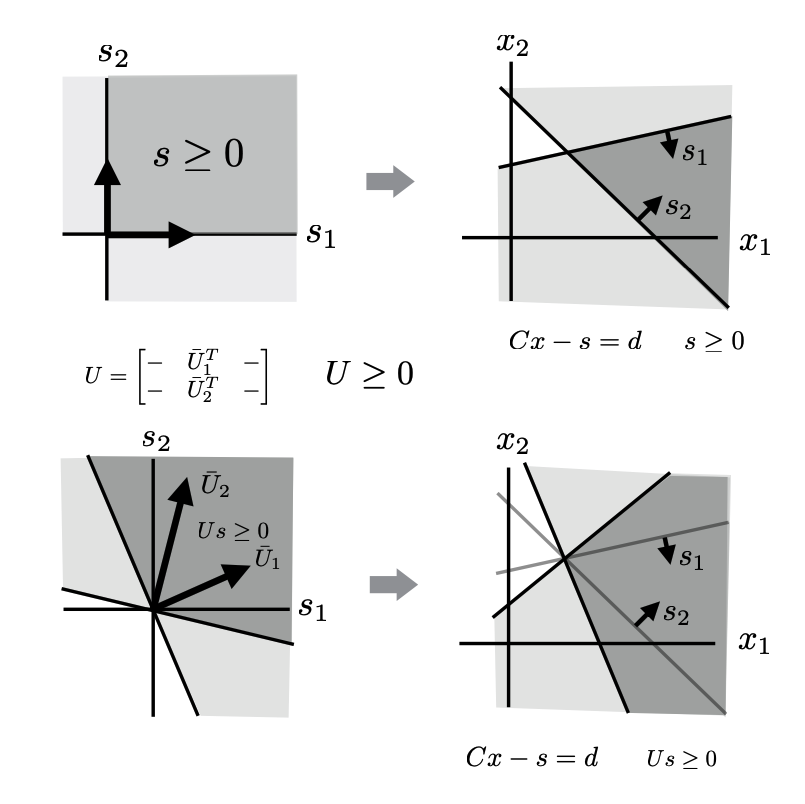
UW Courses: EE578
Offerings: Win21
Topics:
Linear transformations of sets, affine sets - range and nullspace representations, inequality constraints, polytopes, slack variables, linear programs (LP), quadratic programs (QP) Lagrange multipliers, vector space duality, Lagrangian duality - game interpretation LP & QP duality, primal and dual visual interpretations, KKT conditions, complementary slackness, simplex algorithm, gradient descent, Newton's method, barrier methods, interior point methods.
Class notes:
Win21: lec1 lec2 lec3 lec4 lec5 lec6 lec7 lec8 lec9 lec10
Homeworks:
Win21: hw1 hw2 hw3 hw4 hw5 hw6 hw7 hw8
Supplemental:
Topics:
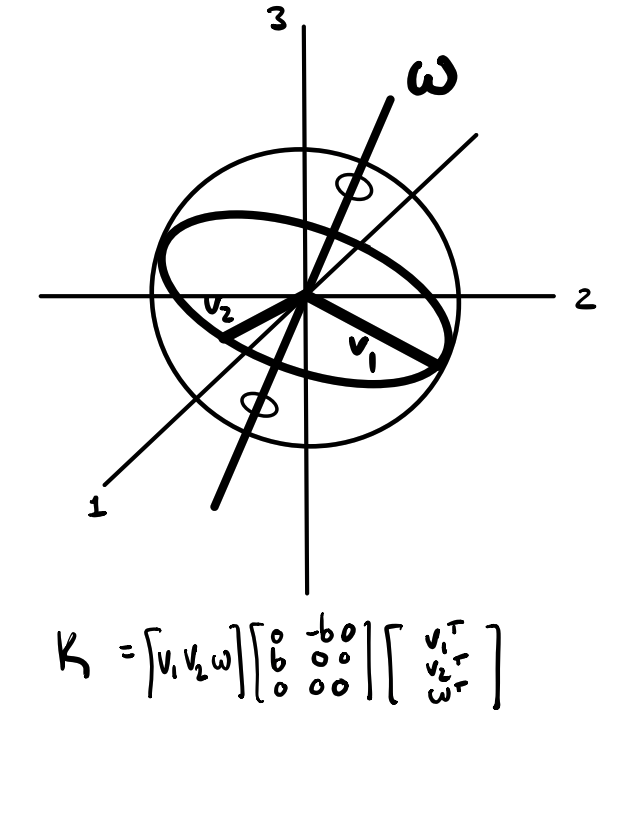
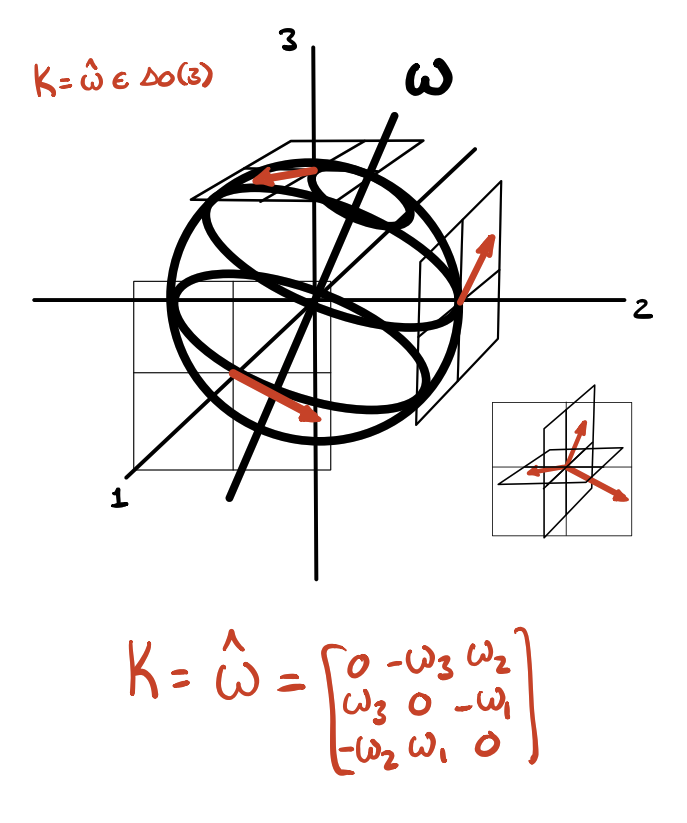
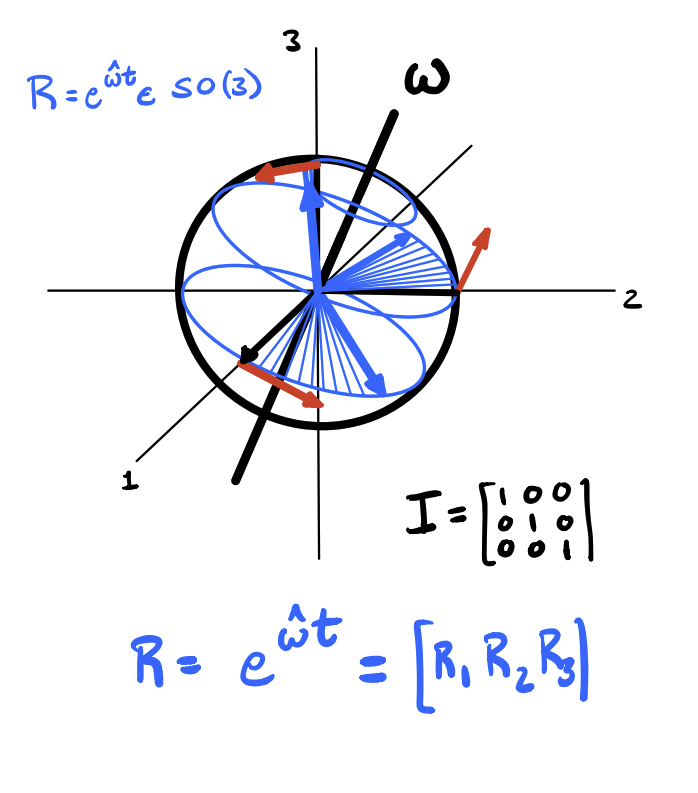
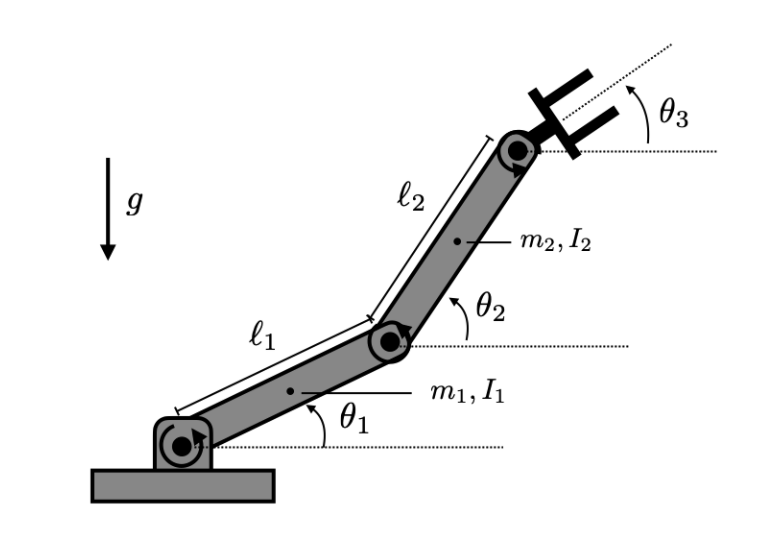
Coordinate transformations, rotations, skew-symmetric matrix exponential, homogeneous transformations, inverting coordinate transforms, Lie groups and lie algebras, SO(3) & so(3), SE(3) & se(3), joint transformations, product of exponentials, forward kinematics, inverse kinematics via Paden-Kahn subproblems, Lagrangian dynamics formulation